Закон больших чисел

Что такое Закон больших чисел?

Закон больших чисел в математике гласит, что выборочное среднее, полученное из набора значений, имеет больше шансов быть ближе к фактическому среднему, чем больше выборочный набор значений. Чем больше число попыток, тем выше вероятность получения точного значения.

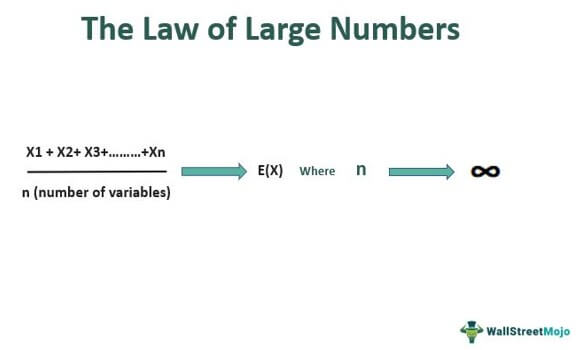
Поэтому выявить истинный потенциал и точные характеристики можно, если взять большую группу образцов. Другими словами, каждый дополнительный след увеличивает шансы получить точное ожидаемое значение. Соответственно, Закон больших чисел имеет широкий спектр применения в реальной жизни.

Оглавление

• Что такое Закон больших чисел?
  • Объяснение закона больших чисел
  • Закон больших чисел в статистике
  • Примеры закона больших чисел
    • Пример №1
    • Пример #2
  • Закон больших чисел в страховании
  • Часто задаваемые вопросы
  • Рекомендуемые статьи

Ключевые выводы

• Закон больших чисел гласит, что чем больше выборка, тем больше вероятность того, что среднее значение выборки будет ближе к среднему распределению.
• Это особенно полезно для аппроксимации огромных вычислений и повышения шансов на точность в заданных настройках. Получение числа, более близкого к фактическому среднему или среднему, повышает надежность данных и может помочь в принятии важных решений.
• Человек может применить его к целому ряду предприятий, включая, среди прочего, оценку премии, устанавливаемой в страховой отрасли, прогнозирование прогнозов роста в корпорации и определение демографических характеристик в статистике.

Объяснение закона больших чисел

Закон больших чисел, или «Золотая теорема», или «Теорема Бернулли» курировал Якоб Бернулли, швейцарский математик. Позднее эта теорема стала известна как «Закон больших чисел». В нем говорится, что неизвестная пропорция может достичь определенной степени точности за соответствующее количество испытаний. Теорема обычно используется для оптимизации размеров выборки. Размер выборки. Формула размера выборки отображает соответствующий диапазон генеральной совокупности, на которой проводится эксперимент или опрос. Он измеряется с использованием размера совокупности, критического значения нормального распределения при требуемом доверительном уровне, доли выборки и предела погрешности. Подробнее и приблизительных вычислений, которые сложны. Он бывает двух типов — сильный закон больших чисел и слабый закон больших чисел.

Слабый закон больших чисел показывает, что если существует набор независимых и одинаково распределенных случайных величин, то выборочное среднее будет сходиться по вероятности к фактическому среднему. Если выборочные средние должны соответствовать среднему распределению, при оценке может использоваться большой выборочный набор значений. Но сильный закон утверждает, что среднее значение выборки и среднее распределение будут сходиться ближе к фактическому значению. Слабый закон и сильный закон больших чисел сильно отличаются друг от друга, и их функции различны.

Закон, однако, отличается от «ошибки игрока», которая представляет собой мыслительный процесс, когда люди предсказывают определенный набор событий, происходящих на основе предыдущего набора обстоятельств. Скажем, в ситуации 50 подбрасываний монеты выпало уже 20 орлов. Человек будет ожидать, что остальные события приведут к выпадению решки, поскольку впереди была выскочка с решкой. Закон больших чисел не поддерживает теорию событий, внезапно развивающую предвзятость по отношению к конкретному событию.

Закон больших чисел в статистике

Закон больших чисел может быть особенно полезен в случае статистики. Актуальность.Подробнее. Например, предположим, что нам нужно определить средний возраст деревни.

Допустим, в этой конкретной деревне проживает около 1000 человек. Если мы возьмем возраст пяти человек, т. е. 20, 30, 40, 50 и 60 лет, сумма всех чисел составит 200. Взяв среднее значение 200/5 (количество всех взятых значений), мы получим среднее значение. значение 40. Следовательно, средний возраст этой группы составляет 40 лет. Эта небольшая выборка из 5 человек слишком мала, чтобы представлять выборку из 1000 человек. Когда имеется большая выборка возрастов, значения варьируются. Допустим, средний возраст 10 человек сейчас составляет 50 лет. Существует очевидный сдвиг значения по сравнению с предыдущим значением в 40 лет. Это более высокое изменение значения будет иметь больше шансов приблизиться к значению фактического среднего возраста населения деревни. Статистика использует аналогичные приложения Закона для определения численности населения, ожидаемой продолжительности жизни и уровня грамотности в стране.

Примеры закона больших чисел

Пример №1

Предположим, есть соревнование по подбрасыванию монеты между двумя людьми, А и В. Победителем становится тот, у кого выпадет больше всего решек. Однако им еще предстоит определить, сколько раз им разрешено подбрасывать монету. Изначально в случае подбрасывания монеты вероятность равна 1/2. т. е. для каждого броска вероятность выпадения решки равна 0,5. Предположим, они подбрасывают монету 20-30 раз, а решка выпадала только семь раз. Перевернув его еще десять раз, можно увеличить счет до 9 решек. Чем больше человек подбрасывает монету, тем больше шансов получить пропорцию решающего отношения, т. е. 0,5.

Пример #2

Предположим, Сэм — инвестор, и есть три известные компании: «ABC», «CDE» и «EFG». Он решает инвестировать в компанию, которая может увеличить свою рыночную стоимость на 50% за короткий период. Скажем, ABC оценивается в 40 миллионов долларов, CDE — в 80 миллионов долларов, а EFG — всего в 4 миллиона долларов. Итак, глядя на них, мы знаем, что 50% для ABC будут дополнительными 20 миллионами долларов; для CDE это будет 40 миллионов долларов. А для EFG это будет увеличение рыночной стоимости на 2 миллиона долларов. Итак, глядя на это, EFG требуется лишь небольшая сумма для роста, и Сэм может выбрать EFG в соответствии с прогнозом роста, который он сделал.

Закон больших чисел в страховании

Закон больших чисел помогает страховым компаниям снизить риск убытков за счет объединения информации о большом количестве людей. Возьмем в качестве примера компанию по страхованию автомобилей ABC Ltd. Компания собирает данные от людей всех возрастов, чтобы собрать информацию об их возрасте и количестве совершенных аварий. Это поможет определить, какую надбавку взимать за конкретную деталь в этой возрастной группе. Например, если причиной несчастных случаев в основном являются люди в возрасте 25 лет, то с лиц, принадлежащих к этой категории, будет взиматься более высокая плата.

Взимание более высоких страховых взносов для этой конкретной возрастной группы может помочь возместить убытки из-за несчастных случаев, вызванных ими. Эти компании приходят к такому выводу, изучив данные многих людей, так как небольшая выборка людей может не содержать требуемых возрастных групп и раскрывать какую-либо важную информацию. В области страхования используются аналогичные приложения в страховании домов, медицинском страховании и других транспортных средствах.

Часто задаваемые вопросы

Как можно использовать Закон больших чисел?

Этот конкретный метод можно использовать в различных отраслях, например, для определения премии, устанавливаемой в страховой отрасли, прогнозирования прогнозов роста в корпорации и т. д.

Что такое слабый и сильный Закон больших чисел?

Определение слабого закона больших чисел гласит, что если существует набор независимых и одинаково распределенных случайных величин, среднее значение выборки будет сходиться к фактическому среднему значению. Выборочное среднее можно приблизить к среднему распределению, используя большой выборочный набор значений. С другой стороны, строгое определение закона больших чисел утверждает, что среднее значение выборки и среднее значение распределения будут сходиться ближе к истинному значению.

Чем полезен Закон больших чисел?

Закон особенно эффективен для аппроксимации больших вычислений и повышения вероятности точности в ситуации. Приближение цифры к реальному среднему или среднему повышает надежность данных и может помочь принять ключевые решения.

Рекомендуемые статьи

Эта статья была руководством по закону больших чисел и его определению. Здесь мы обсуждаем закон больших чисел в статистике и страховании вместе с его примерами. Вы можете узнать больше о статистике из следующих статей –

• Описательная статистика
• Мультиколлинеарность
• Рассеивание