Односторонний тест

Определение одностороннего теста

Односторонний тест — это метод статистической проверки гипотез. Чтобы отвергнуть нулевую гипотезу, среднее значение выборки должно быть больше или меньше среднего значения генеральной совокупности. Этот тест также называют тестом направления или гипотезой направления. Тест выполняется, чтобы доказать истинность или ложность утверждения.

Определение этого теста не может быть двусмысленным, а это означает, что он может быть меньше или больше, чем среднее значение генеральной совокупности, но не может быть и тем, и другим. Проверка гипотез определяет вероятность того, что гипотеза окажется верной. Тест подтверждает точность альтернативной гипотезы, устраняя случайность.

Оглавление

• Определение одностороннего теста
  • Объяснение однохвостого теста
  • Пример
  • Односторонний тест против двустороннего теста
  • Часто задаваемые вопросы (FAQ)
  • Рекомендуемые статьи

Ключевые выводы

• Для односторонней проверочной гипотезы среднее значение выборки может быть больше или меньше среднего значения генеральной совокупности, но не может быть и тем, и другим одновременно.
• Нулевая гипотеза и альтернативная гипотеза предшествуют односторонним тестам вместе с p-значением (значением вероятности).
• Тест направленный; следовательно, он не рассматривает другое направление при установлении отношений.

Объяснение однохвостого теста

Односторонний тест – это статистический метод проверки гипотез. Основываясь на статистических данных, проверка гипотез определяет, верна ли теория или нет. Если тест показывает, что средняя выборка одновременно больше и меньше генеральной совокупности, это двусторонний тест. Но когда тест показывает, что среднее значение выборки только больше или меньше генеральной совокупности, это односторонний тест. Так, при тестировании, если данные выборки встречаются преимущественно с одной стороны, то нулевая гипотезаНулевая гипотезаНулевая гипотеза предполагает, что данные выборки и данные совокупности не имеют различий, или, говоря простым языком, предполагает, что утверждение, сделанное человеком относительно данных или население является абсолютной истиной и всегда право. Таким образом, даже если выборка будет взята из генеральной совокупности, результат, полученный в результате изучения выборки, будет таким же, как и предположение. Читать далее будет отвергнуто — будет принята альтернативная гипотеза.

Односторонним тестам предшествуют нулевая гипотеза и альтернативная гипотеза. От исследователей требуется доказать ошибочность нулевой гипотезы; только тогда они могут претендовать на альтернативную гипотезу. В идеале, чтобы доказать теорию, исследователям необходимо исключить случайность. Когда они доказывают наблюдение, вызванное определенной причиной, наблюдения не должны быть вызваны случайными факторами. Уровни случайности определяются статистической значимостьюСтатистическая значимостьСтатистическая значимость — это вероятность того, что наблюдение не вызвано ошибкой выборки.Подробнее.

Уровень значимости представлен как «p», что означает вероятность. Обычно значения значимости составляют 1%, 5% или 10%. Однако исследователи могут по своему усмотрению использовать любую другую вероятность. Значение вероятности рассчитывается в предположении, что нулевая гипотеза верна. Чем ниже p-valueP-valueP-Value, или значение вероятности, это решающий фактор для нулевой гипотезы для вероятности того, что предполагаемый результат окажется истинным, будет принят или отклонен, и принятия альтернативного результата в случае предполагаемого отказ от результатов. читай больше, тем меньше случайность — нулевая гипотеза легко окажется ложной. Если результирующее значение p ниже 5%, разница между обоими наблюдениями является статистически значимой, и нулевая гипотеза отклоняется.

Пример

Давайте разберемся с применением односторонних тестов на примере.

Предположим, директор школы хочет доказать, что новый профессор математики повысил успеваемость в классе на 9,29%. Директор выдвинул нулевую (H0) и альтернативную (Ha) гипотезы:

Н0: мк ≤ 9,29

Га: м > 9,29

Принципал надеется отвергнуть нулевую гипотезу и подтвердить свое утверждение в качестве альтернативной гипотезы. Если тест отклоняет нулевую гипотезу, поддерживается альтернативная гипотеза. Напротив, если результат теста не опровергает нулевую гипотезу, директору придется провести дополнительные исследования, чтобы найти другие объяснения успеваемости в классе.

Область отбраковки находится на одной стороне распределения выборки. Распределение выборки. Распределение выборки — это вероятностное распределение, использующее статистику, когда сначала выбирают конкретную совокупность, а затем используют случайные выборки, взятые из совокупности. Он нацелен на распространение частот, связанных с распространением различных результатов или результатов, которые могут иметь место для конкретной выбранной группы населения. Подробнее. Таким образом, чтобы определить, как класс работает по сравнению с другим профессором математики, директор должен провести правосторонний тест значимости — экстремальные значения должны приходиться на правую сторону кривой нормального распределения. Нормальное распределение Нормальное распределение Нормальное распределение — это колоколообразная кривая распределения частот, которая помогает описать все возможные значения, которые случайная величина может принимать в заданном диапазоне, при этом большая часть области распределения находится в середине, а небольшая часть — в хвостах, на крайних точках. Это распределение имеет два ключевых параметра: среднее значение (µ) и стандартное отклонение (σ), которые играют ключевую роль в расчете доходности активов и в стратегии управления рисками. переменные распределяются симметрично. Эти значения равномерно распределены слева и справа от центральной тенденции. Центральная тенденция. Центральная тенденция — это статистическая мера, которая отображает центральную точку всего распределения данных, и вы можете найти ее с помощью 3 различных мер, т. е. среднего, медианы и режима. .читать далее. Таким образом, формируется колоколообразная кривая.

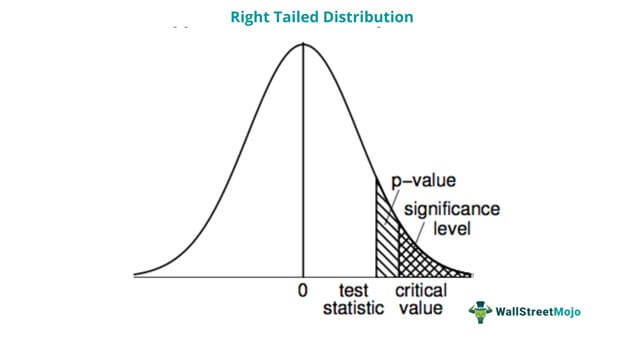
Результаты теста с одним хвостом, представленные в правой области кривой, могут показать совпадение между повышением успеваемости в классе и периодом, преподаваемым новым профессором. Далее тест покажет, существенно ли отличались результаты предыдущего профессора.

Односторонний тест против двустороннего теста

Односторонний тестДвухсторонний тест В односторонних тестах альтернативные гипотезы имеют только один конец. В двустороннем тесте альтернативная гипотеза имеет два конца. Это направленная гипотеза. Это ненаправленная гипотеза. Область отклонения может быть либо левой, либо правой. Область отторжения может быть как левой, так и правой. Существует связь между переменными в одном направлении. Связь между переменными существует в любом направлении. Результат всегда больше или меньше определенного значения. Результат больше или меньше определенного диапазона значений. Обозначается > или < Обозначается как ≠

Часто задаваемые вопросы (FAQ)

Когда использовать односторонние тесты?

Односторонние тесты используются в ситуациях, когда теория или утверждение должны быть либо истинными, либо ложными. Предположим, что разработано новое лекарство. Разработчики хотят проверить, является ли он более эффективным, чем текущий препарат. В таких сценариях можно использовать один хвостовой тест для доказательства эффективности.

На какой гипотезе основан односторонний критерий?

Он основан на двух гипотезах — нулевой гипотезе и альтернативной гипотезе. Тест подтвердит только одно из них. Исследователи хотят доказать ложность нулевой гипотезы, чтобы установить свои выводы в качестве альтернативного объяснения выборочных данных.

Каковы преимущества использования односторонних и двусторонних тестов?

Тесты с одним хвостом имеют очень практическое преимущество — для получения значимости требуется меньше испытуемых. С другой стороны, двусторонний тест разделяет уровень значимости, а затем подразумевает его в обоих направлениях. Таким образом, каждое направление в два раза слабее теста с одним хвостом.

Рекомендуемые статьи

Эта статья была руководством к тому, что такое односторонний тест и определение. Здесь мы обсуждаем примеры односторонних тестов, графики, p-значения и то, чем они отличаются от двусторонних тестов. Вы можете узнать больше о финансировании из следующих статей –

• T-тест в Excel
• Z-тест в Excel
• P-значение в Excel