Формула Z-теста

Формула для расчета Z-теста в статистике

Z-тест в статистике относится к проверке гипотезы, используемой для определения того, различаются ли рассчитанные средние значения двух выборок в случае, если доступны стандартные отклонения и выборка велика.

Искусственный интеллект поможет тебе заработать!

Подписывайся на канал "Виртуальный Каппер" и получай точные и бесплатные прогнозы на спорт от искусственного интеллекта.

Z = (х – м) / Привет

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

где x = любое значение из совокупности

μ = среднее значение населения
ơ = стандартное отклонение населения

В случае выборки формула для статистики значения Z-теста рассчитывается путем вычитания среднего значения выборки из значения X. Затем результат делится на стандартное отклонение выборки. Математически это представляет как

Z = (х – x_среднее) / с

где

x = любое значение из выборки
х_среднее = выборочное среднее
s = стандартное отклонение выборки

Оглавление

Формула для расчета Z-теста в статистике

Расчет Z-теста (шаг за шагом)

Формула для статистики Z-теста для населения выводится с использованием следующих шагов:

Во-первых, вычислите средние значения совокупности и стандартное отклонение на основе наблюдения, зафиксированного в среднем значении совокупности, и каждое наблюдение обозначается xi. Тогда общее количество наблюдений в популяции обозначается через N.
Средняя численность населения,
Стандартное отклонение населения,
Наконец, статистика Z-теста вычисляется путем вычитания среднего значения совокупности из переменной. Затем результат делится на стандартное отклонение генеральной совокупности, как показано ниже.
Z = (х – мк) /
Формула статистики Z-теста для выборки получается из следующих шагов:
Во-первых, рассчитайте среднее значение выборки и стандартное отклонение так же, как указано выше. Здесь общее количество наблюдений в выборке обозначается n таким образом, что n < N.
Выборочное среднее,
Стандартное отклонение выборки,
Наконец, статистика Z-теста рассчитывается путем вычитания среднего значения выборки из значения X. Затем результат делится на стандартное отклонение выборки, как показано ниже.
Z = (x – x_mean) / с

Примеры

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel с формулой Z Test здесь – Шаблон Excel с формулой Z-теста

Пример №1

Предположим, что в школе есть учащиеся, явившиеся на классный тест. Средний балл в тесте — 75, а стандартное отклонение — 15. Но сначала определите Z-тест Дэвида, который набрал 90 баллов.

Данный

Среднее значение населения, μ = 75
Стандартное отклонение населения, ơ = 15

Следовательно, можно рассчитать статистику Z-теста как

Z = (90 – 75) / 15

Статистика Z-теста будет –

Z = 1

Таким образом, результат теста Дэвида на одно стандартное отклонение выше среднего балла генеральной совокупности, т. е. в соответствии с z-оценкой. данные, которые помогают проверить рассматриваемую гипотезу. Другими словами, это расстояние точки данных от среднего значения генеральной совокупности, выраженное как кратное стандартному отклонению. 84,13% учащихся набрали меньше баллов, чем Дэвид.

Пример #2

Возьмем, к примеру, 30 студентов, отобранных в качестве части выборочной группы, опрошенной, чтобы узнать, сколько карандашей они использовали за неделю. Определить балл Z-теста для 3-го ученика на основе данных ответов: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

Данный,

x = 5, так как ответ третьего ученика равен 5
Объем выборки, n = 30

Выборочное среднее, = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30

Среднее значение = 4,17

Можно рассчитать стандартное отклонение выборки, используя приведенную выше формулу.

э = 1,90

Следовательно, можно рассчитать балл Z-теста для третьего ученика как:

Z = (х – х) / с

Z = (5 –17) / 1,90
Z = 0,44

Таким образом, использование 3-м учащимся в 0,44 раза превышает стандартное отклонение по сравнению со средним значением использования выборки, т. е. согласно таблице Z-показателей, 67% учащихся используют меньше карандашей, чем 3-й учащийся.

Пример №3

Возьмем, к примеру, 30 студентов, отобранных в качестве части выборочной группы, которая провела опрос, чтобы узнать, сколько карандашей было использовано за неделю. Определить балл Z-теста для 3-го ученика на основе данных ответов: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

Ниже приведены данные для расчета статистики Z-теста.

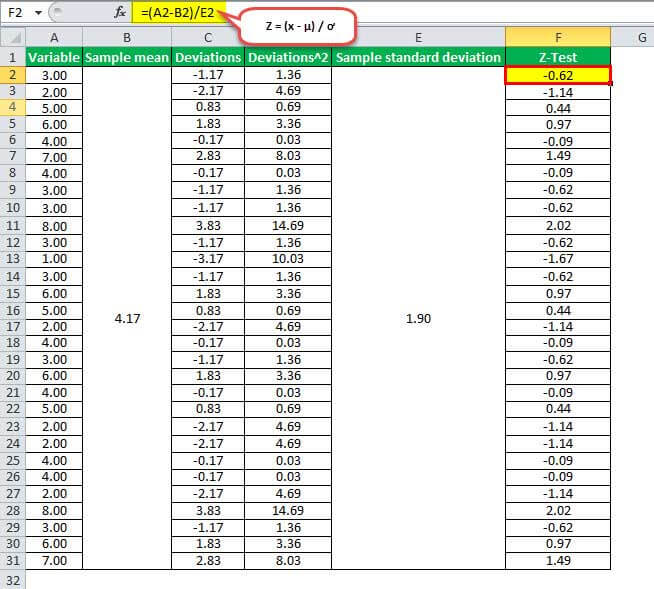
Вы можете обратиться к листу Excel ниже для подробного расчета статистики Z-теста.

Актуальность и использование

Важно понимать концепцию статистики Z-теста, потому что она обычно используется всякий раз, когда возникают споры о том, следует ли тестовая статистика нормальному распределению. может находиться в заданном диапазоне, при этом большая часть области распространения находится в середине, а немногие – в хвостах, на крайних точках. Это распределение имеет два ключевых параметра: среднее значение (µ) и стандартное отклонение (σ), которые играют ключевую роль в расчете доходности активов и в стратегии управления рисками. Подробнее читайте в соответствующей нулевой гипотезе. Однако следует помнить, что использовать Z-тест можно только в том случае, если размер выборки превышает 30. В противном случае можно использовать t-тестT-тестТ-тест — это метод определения того, отличаются ли средние значения двух групп друг от друга. существенно. Это метод логической статистики, облегчающий проверку гипотез. Подробнее.

Формула Z-теста

Формула для расчета Z-теста в статистике