Средняя геометрическая доходность

Что такое средняя геометрическая доходность?

Среднегеометрическая доходность рассчитывает средний доход от инвестиций, которые складываются на основе его частоты в зависимости от периода времени, и используется для анализа эффективности инвестиций, поскольку указывает доход от инвестиций.

Оглавление

Что такое средняя геометрическая доходность?

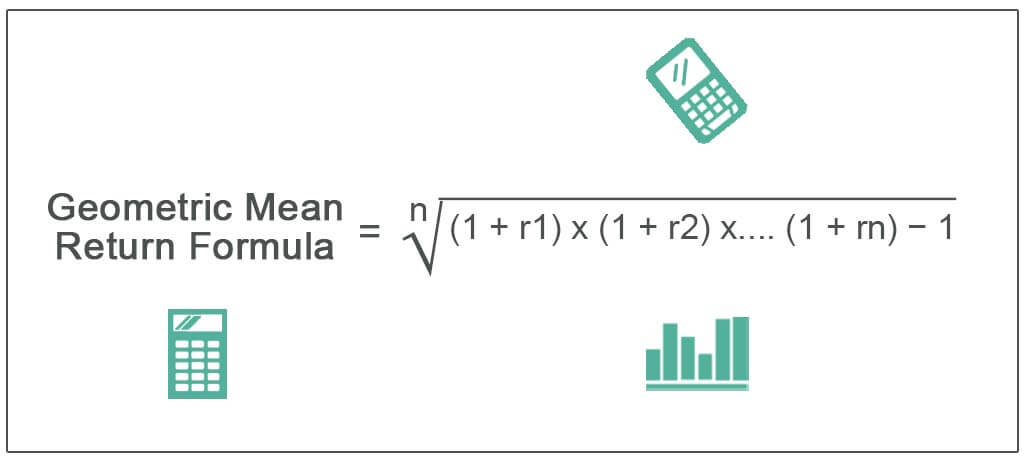
Формула среднего геометрического возврата

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

г = норма прибыли
n = количество периодов

Это средний набор продуктов, технически определяемый как n-й корневой продукт ожидаемого количества периодов. Основное внимание в расчете уделяется представлению «сравнения яблока с яблоком» при рассмотрении двух похожих вариантов инвестиций.

Примеры

Разберем формулу на примере:
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%}

Вы можете скачать этот шаблон Excel для среднего геометрического возврата здесь – Шаблон Excel для среднего геометрического возврата

Предполагая доход от 1000 долларов на денежном рынке Денежный рынок Денежный рынок – это финансовый рынок, на котором краткосрочные активы и открытые фонды торгуются между учреждениями и трейдерами.Подробнее, который зарабатывает 10% в первый год, 6% во второй год. , и 5% в третий год, средняя геометрическая доходность будет:

Это средний доход с учетом начисления сложных процентовНачисление сложных процентовНачисление сложных процентов представляет собой метод инвестирования, при котором доход, полученный в результате инвестиций, реинвестируется, а новая основная сумма увеличивается на сумму реинвестированного дохода. В зависимости от срока вклада к основной сумме добавляются проценты. Подробнее эффект. Если бы это была простая средняя доходность, она взяла бы сумму заданных процентных ставок и разделила бы ее на 3.

Таким образом, чтобы получить стоимость в 1000 долларов через 3 года, доход будет составлять 6,98% каждый год.

1 год

Проценты = 1000 долларов США * 6,98% = 69,80 долларов США.
Основная сумма = 1000 долларов США + 69,80 долларов США = 1069,80 долларов США.

2 год

Проценты = 1069,80 долл. США * 6,98% = 74,67 долл. США.
Основная сумма = 1069,80 долл. США + 74,67 долл. США = 1144,47 долл. США

3 год

Проценты = 1144,47 долл. США * 6,98% = 79,88 долл. США.
Основная сумма = 1 144,47 доллара США + 79,88 доллара США = 1 224,35 доллара США.
Таким образом, окончательная сумма через 3 года составит 1 224,35 доллара США, что будет равно сумме основного долга с использованием трех отдельных процентов, начисляемых ежегодно.

Рассмотрим другой пример для сравнения:

Инвестор держит акции, которые были волатильными, доходность которых значительно менялась от года к году. Первоначальные инвестиции составляли 100 долларов в акции А, и они вернули следующее:

1-й год: 15 %

Год 2: 160%

3-й год: -30%

4-й год: 20 %

Среднее арифметическое будет = [15 + 160 – 30 + 20] / 4 = 165/4 = 41,25%

Однако истинная отдача будет:

Год 1 = 100 долларов * 15% [1.15] = 15 долларов = 100 + 15 = 115 долларов
Год 2 = 115 долларов * 160% [2.60] = 184 доллара = 115 + 184 = 299 долларов
3-й год = 299 долл. США * -30% [0.70] = 89,70 долл. США = 299 – 89,70 = 209,30 долл. США
Год 4 = 209,30 долл. США * 20% [1.20] = 41,86 доллара США = 209,30 + 41,86 = 251,16 доллара США.

Результирующее среднее геометрическое в этом случае будет равно 25,90%. Это намного ниже, чем среднее арифметическое 41,25%.

Проблема со средним арифметическим заключается в том, что он имеет тенденцию значительно завышать фактическую среднюю доходность. В приведенном выше примере было замечено, что во второй xгод доходность выросла на 160%, а затем упала на 30%, что соответствует годовой дисперсии на 190%.

Таким образом, Среднее арифметическое Среднее арифметическое Среднее арифметическое обозначает среднее значение всех наблюдений ряда данных. Это совокупность всех значений в наборе данных, деленная на общее количество наблюдений. Читать далее легко использовать и вычислять, и это может быть полезно при попытке найти среднее значение для различных компонентов. Тем не менее, это неуместный показатель для определения фактической средней рентабельности инвестиций. Среднее геометрическое Среднее геометрическое Среднее геометрическое (GM) — это метод центральной тенденции, который определяет среднее значение мощности данных ряда роста. читать далее очень полезно для измерения производительности портфеля.

Использование

Использование и преимущества формулы среднего геометрического дохода:

Этот доход специально используется для инвестиций, которые составляются. Простые процентыПростые процентыПростые проценты (SI) относятся к проценту процентов, начисленных или полученных на основную сумму за определенный период. Подробнее счет будет использовать среднее арифметическое для упрощения.
Его можно использовать для разбивки эффективной ставки за период владения доходом. Доход периода владения. Доход периода владения относится к общей доходности за период, в течение которого инвестиции удерживались, обычно выражаемой в процентах от первоначальных инвестиций, а также для сравнения доходов от различных инвестиций, удерживаемых для разных периоды времени.Подробнее.
Он используется для текущей стоимости и будущей стоимости. Будущая стоимость Формула будущей стоимости (FV) — это финансовая терминология, используемая для расчета стоимости денежного потока на футуристическую дату по сравнению с исходным чеком. Цель уравнения FV состоит в том, чтобы определить будущую стоимость предполагаемых инвестиций и принесут ли доходы достаточную прибыль, чтобы учесть временную стоимость денег. Подробнее о формулах денежных потоков.

Калькулятор средней геометрической доходности

Вы можете использовать следующий калькулятор.

.cal-tbl td{ верхняя граница: 0 !важно; }.cal-tbl tr{ высота строки: 0.5em; } Только экран @media и (минимальная ширина устройства: 320 пикселей) и (максимальная ширина устройства: 480 пикселей) { .cal-tbl tr{ line-height: 1em !important; } } r1 (%) r2 (%) r3 (%) Формула возврата среднего геометрического =

Формула среднего геометрического возврата = 3√(1 + r1) * (1 + r2) * (1 + r3) – 1 = 3√(1 + 0) * (1 + 0) * (1 + 0) – 1 = 0

Формула среднего геометрического возврата в Excel (с шаблоном Excel)

Давайте теперь сделаем тот же пример выше в Excel. Это очень просто. Вам необходимо предоставить два входа: «Количество чисел» и «Количество периодов».

Вы можете легко рассчитать среднее геометрическое в предоставленном шаблоне.

Таким образом, чтобы получить стоимость в 1000 долларов через 3 года, доход будет составлять 6,98% каждый год.

Таким образом, окончательная сумма через 3 года составит 1 224,35 доллара США, что будет равно начислению основной суммы с использованием 3 отдельных процентов, начисляемых ежегодно.

Рассмотрим другой пример для сравнения: