Квартильное отклонение

Что такое квартильное отклонение?

Квартильное отклонение зависит от разницы между первым квартилем и третьим квартилем в частотном распределении. Разница также известна как межквартильный диапазон. Разница, деленная на два, известна как квартильное отклонение или полумежквартильный диапазон.

Если взять половину разницы или дисперсии между 3-м квартилем и 1-м квартилем простого распределения или частотного распределения, это будет квартильное отклонение.

Оглавление

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

Что такое квартильное отклонение?

Формула

Формула квартильного отклонения (QD) используется в статистике для измерения спреда или, другими словами, для измерения дисперсии. Его также можно назвать полуинтерквартильным диапазоном.

QD = Q3 – Q1 / 2

Формула включает в расчет Q3 и Q1, которые представляют собой верхние 25% и нижние 25% данных соответственно. Когда разница между этими двумя значениями и это число уменьшается вдвое, оно дает меру распространения или дисперсии.
Таким образом, чтобы рассчитать квартильное отклонение, вам нужно сначала найти Q1, затем второй шаг — найти Q3, затем провести разницу между обоими, и последний шаг — разделить на 2.
Это один из лучших методов дисперсии открытых данных.

Примеры

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel с формулой квартильного отклонения здесь – Формула квартильного отклонения Шаблон Excel

Пример №1

Рассмотрим набор данных из следующих чисел: 22, 12, 14, 7, 18, 16, 11, 15, 12. Вам необходимо рассчитать квартильное отклонение.

Решение:

Во-первых, нам нужно упорядочить данные в порядке возрастания, чтобы найти Q3 и Q1 и избежать дублирования.

7, 11, 12, 13, 14, 15, 16, 18, 22

Расчет Q1 можно выполнить следующим образом:

Q1 = ¼ (9 + 1)

=¼ (10)

Q1“=”2.5 Срок

Расчет Q3 можно выполнить следующим образом:

Q3=¾ (9 + 1)

=¾ (10)

Q3“=” 7.5 Срок

Расчет квартильного отклонения можно выполнить следующим образом:

Q1 представляет собой среднее значение 2-го, что равно 11, и добавляет разницу между 3-м и 4-м и 0,5, что составляет (12-11) * 0,5 = 11,50.
Q3 – это 7-й член и произведение 0,5. Разница между 8-м и 7-м членами составляет (18-16)*0,5, а результат равен 16 + 1 = 17.

QD = Q3 – Q1 / 2

Используя формулу квартильного отклонения, имеем (17-11,50)/2

=5,5/2

QD“=”2,75.

Пример #2

Harry Ltd. является производителем текстиля и работает над структурой вознаграждения. Руководство обсуждает начало новой инициативы, но сначала они хотят знать, насколько велик их производственный спред.

Руководство собрало среднесуточные данные о производительности за последние десять дней в расчете на одного (среднего) работника.

155, 169, 188, 150, 177, 145, 140, 190, 175, 156.

Используйте формулу квартильного отклонения, чтобы помочь руководству найти дисперсию.

Решение:

Количество наблюдений здесь равно 10, и нашим первым шагом было бы упорядочить данные n по возрастанию.

140, 145, 150, 155, 156, 169, 175, 177, 188, 190

Расчет Q1 можно выполнить следующим образом:

Q1= ¼ (n+1)-й член

=¼ (10+1)

=¼ (11)

Q1“=” 2.75-й срок

Расчет Q3 можно выполнить следующим образом:

Q3= ¾ (n+1)-й член

=¾ (11)

Q3“=” 8.25 Срок

Расчет квартильного отклонения можно выполнить следующим образом:

2-й член равен 145, а теперь добавляем к этому 0,75 * (150 – 145), что составляет 3,75, и результат равен 148,75.
8-й член равен 177, а теперь добавляем к этому 0,25 * (188 – 177), что равно 2,75, и результат равен 179,75.

QD = Q3 – Q1 / 2

Используя формулу квартильного отклонения, имеем (179,75-148,75)/2

=31/2

QD“=”15.50.

Пример №3

Международная академия Райана хочет проанализировать, сколько процентных оценок распределяют их студенты.

Данные для 25 студентов.

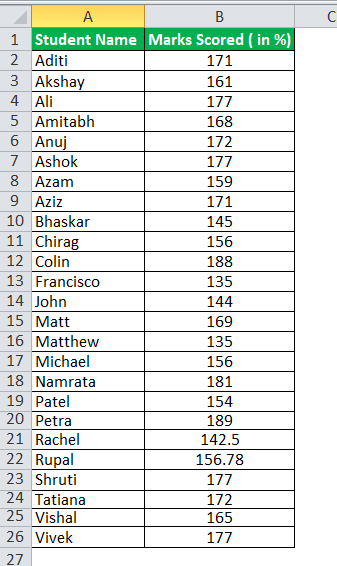
Используйте формулу Quartile Deviation, чтобы узнать дисперсию оценок в %.

Решение:

Количество наблюдений здесь равно 25. Итак, нашим первым шагом было бы упорядочить данные в порядке возрастания.

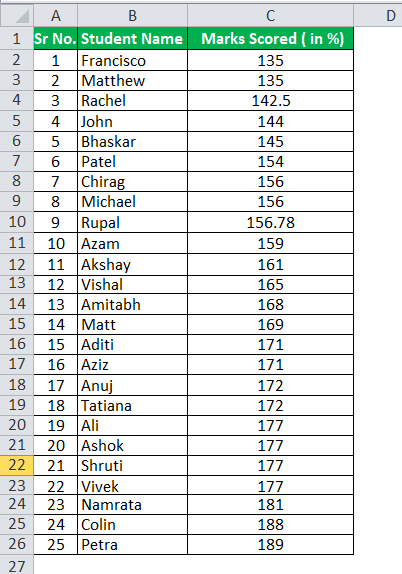
Расчет Q1 можно выполнить следующим образом:

Q1= ¼ (n+1)-й член

=¼ (25+1)

=¼ (26)

Q1“=” 6,5-й срок

Расчет Q3 можно выполнить следующим образом:

Q3=¾ (n+1)-й член

=¾ (26)

Q3 “=” 19.50 Срок

Расчет квартильного отклонения или полуинтерквартильного диапазона можно выполнить следующим образом:

6-й член равен 154 и теперь добавляем к этому 0,50 * (156 – 154), что равно 1, и результат равен 155,00.
19-й член равен 177, а теперь добавляем к этому 0,50 * (177 – 177), что равно 0, и результат равен 177.

QD = Q3 – Q1 / 2

Используя формулу квартильного отклонения, имеем (177-155)/2

=22/2

QD“=” 11.

Пример №4

Давайте теперь определим значение с помощью шаблона Excel для практического примера I.

Решение:

Используйте следующие данные для расчета квартильного отклонения.

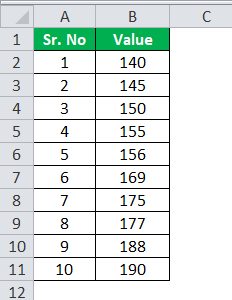
Расчет Q1 можно выполнить следующим образом:

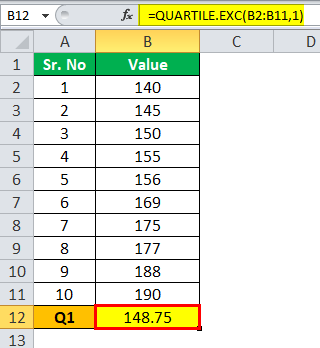
Q1“=”148,75

Расчет Q3 можно выполнить следующим образом:

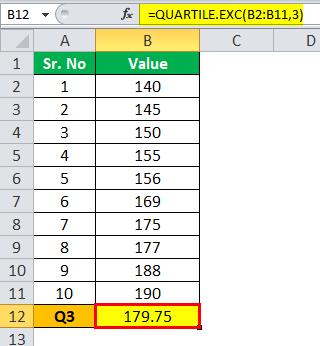
Q3“=” 179,75

Расчет квартильного отклонения можно выполнить следующим образом:

Используя формулу квартильного отклонения, мы имеем (179,75-148,75)/ 2

КД будет –

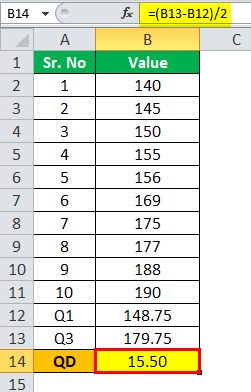
QD “=” 15.50

Актуальность и использование

Квартильное отклонение также известно как полумежквартильный диапазон. Опять же, разница в дисперсии между 3-м и 1-м квартилями известна как межквартильный размах. Межквартильный диапазон показывает степень отклонения наблюдений или значений данного набора данных от среднего или их среднего значения. Квартильное отклонение или полумежквартильный диапазон чаще всего используется в случае, когда кто-то хочет узнать или сказать исследование о дисперсии наблюдений или выборок заданных наборов данных, которые лежат в основной или средней части данного ряда. . Этот случай обычно происходит в распределении, где данные или наблюдения имеют тенденцию сильно лежать в основной части или середине данного набора данных или ряда. Распределение или значения не лежат в крайних точках. Если они лгут, то большого значения для расчета не имеют.