Формула стандартного отклонения

Что такое формула стандартного отклонения?

Стандартное отклонение (SD) — популярный статистический инструмент, обозначаемый греческой буквой «σ». Он измеряет степень вариации или дисперсии набора значений данных по отношению к его среднему (среднему), тем самым интерпретируя надежность данных. Если меньше, точки данных лежат близко к среднему значению, что свидетельствует о надежности. Но если он больше, точки данных расходятся далеко от среднего.

Формула стандартного отклонения ниже

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

Где:

xi = значение каждой точки данных
х̄ = среднее значение
N = количество точек данных

Стандартное отклонение наиболее широко используется и практикуется в службах управления портфелем. Например, управляющие фондами часто используют этот базовый метод для расчета и обоснования своей дисперсии доходности в конкретном портфеле.
Высокое стандартное отклонение портфеляСтандартное отклонение портфеляСтандартное отклонение портфеля относится к волатильности портфеля, рассчитанной на основе трех основных факторов: стандартного отклонения каждого из активов, присутствующих в общем портфеле, соответствующего веса этого отдельного актива и корреляции. между каждой парой активов портфеля. Читать далее означает большую разницу в данном количестве акций в конкретном портфеле. С другой стороны, низкое стандартное отклонение означает меньшую дисперсию запасов между собой.
Не склонный к риску инвестор будет готов пойти на любой дополнительный риск только в том случае, если он компенсирует этот конкретный риск равной или большей прибылью.
Более склонный к риску инвестор может быть не доволен своим стандартным отклонением. В результате они захотят добавить более безопасные инвестиции, такие как государственные облигации или акции крупных компаний. эти акции менее рискованны, чем другие, и стабильны. Они также приносят хорошие дивиденды и доход, и это самый безопасный способ инвестировать в портфель или взаимные фонды, чтобы диверсифицировать риск портфеля и его стандартное отклонение и дисперсию.
Дисперсия и тесно связанное с ней стандартное отклонение измеряют, насколько разбросано распределение. Другими словами, они являются мерами изменчивости.

Оглавление

Что такое формула стандартного отклонения?

Шаги для расчета стандартного отклонения

Выполните следующие шаги:

Во-первых, среднее значение наблюдений вычисляется так же, как и среднее, путем добавления всех точек данных, доступных в наборе данных, и деления его на количество наблюдений.
Затем отклонение от каждой точки данных измеряет среднее значение. Это может быть положительное или отрицательное число, значение возводится в квадрат, а результат вычитается на единицу.
Квадрат дисперсии, рассчитанный на шаге 2, используется для расчета стандартного отклонения.

Примеры

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel формулы стандартного отклонения здесь – Формула стандартного отклонения Шаблон Excel

Пример 1

Точки данных: 1,2 и 3. Каково стандартное отклонение данного набора данных?

Решение:

Используйте следующие данные для расчета стандартного отклонения.

Таким образом, расчет дисперсии будет –

Дисперсия = 0,67

Расчет стандартного отклонения будет –

Стандартное отклонение = 0,82

Пример #2

Найдите стандартное отклонение 4,9,11,12,17,5,8,12,14.

Решение:

Используйте следующие данные для расчета стандартного отклонения.

Расчет среднего будет –

Сначала найдите среднее значение точки данных 4+9+11+12+17+5+8+12+14/9.

Среднее = 10,22

Таким образом, расчет дисперсии будет –

Дисперсия будет –

Дисперсия = 15,51

Расчет стандартного отклонения будет –

Стандартное отклонение = 3,94

Дисперсия = Квадратный кореньКвадратный кореньФункция квадратного корня — это арифметическая функция, встроенная в Excel, которая используется для определения квадратного корня из заданного числа. Чтобы использовать эту функцию, введите термин =SQRT и нажмите клавишу табуляции, которая вызовет функцию SQRT. Более того, эта функция принимает один аргумент стандартного отклонения.

Пример №3

Используйте следующие данные для расчета стандартного отклонения.

Таким образом, расчет дисперсии будет –

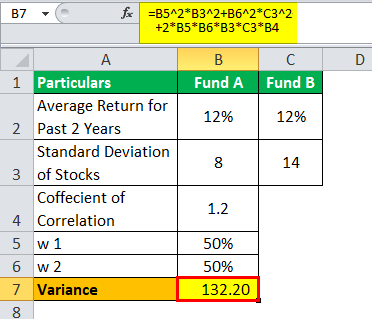
Дисперсия = 132,20

Расчет стандартного отклонения будет –

Стандартное отклонение = 11,50

Менеджеры портфелей часто используют этот тип расчета для расчета риска и доходности портфеля.

Актуальность и использование

Стандартное отклонение исторически полезно при анализе общего риска и доходности матрицы портфеля. Он широко используется и практикуется в промышленности. Корреляция и веса акций портфеля могут влиять на стандартное отклонение портфеля.
В соответствии с соотношением двух классов активов классы активов классифицируются по различным классам в зависимости от их типа, цели или основы доходности или рынков. Основные средства, акционерный капитал (инвестиции в акционерный капитал, сберегательные схемы, связанные с акционерным капиталом), недвижимость, товары (золото, серебро, бронза), денежные средства и их эквиваленты, деривативы (акции, облигации, долговые обязательства) и альтернативные инвестиции, такие как хедж-фонды и биткойны. являются примерами. Подробнее в портфеле снижает риск портфеля, нет необходимости всегда, чтобы одинаково взвешенный портфель обеспечивал наименьший риск во вселенной.
Высокое стандартное отклонение может быть мерой волатильности, но это не обязательно означает, что такой фонд хуже, чем фонд с низким стандартным отклонением. Например, если первый фонд гораздо более эффективен, чем второй, отклонение не будет иметь большого значения.
Стандартное отклонение также используется в статистике. преподают профессора различных ведущих университетов мира. Однако формула для стандартного отклонения изменяется, когда ее используют для расчета выборочного отклонения.
- Уравнение для SD в Sample = просто знаменатель уменьшается на 1.