Формула продолжительности

Что такое формула продолжительности?

Формула дюрации является мерой чувствительности облигации к изменениям процентной ставки и рассчитывается путем деления суммы дисконтированных будущих денежных поступлений по облигации и соответствующего количества лет на сумму дисконтированных будущих денежных потоков. inflowDiscounted Future Cash InflowАнализ дисконтированных денежных потоков — это метод анализа текущей стоимости компании, инвестиций или денежных потоков путем корректировки будущих денежных потоков с учетом временной стоимости денег. Этот анализ оценивает текущую справедливую стоимость активов, проектов или компаний, принимая во внимание многие факторы, такие как инфляция, риск и стоимость капитала, а также анализируя будущие результаты деятельности компании.Подробнее. Приток денежных средств в основном состоит из выплаты купона и погашения в конце. Он также известен как дюрация МаколеяДюрация МаколеяДюрация Маколея — это количество времени, которое требуется инвестору, чтобы вернуть свои вложенные в облигацию деньги за счет купонов и погашения основной суммы. Это средневзвешенное значение периода, в течение которого инвестор должен инвестировать в ценные бумаги, чтобы текущая стоимость денежных потоков от инвестиций равнялась сумме, уплаченной за облигацию. Подробнее.

Математически уравнение длительности представлено следующим образом:

Формула продолжительности = [ ∑in-1 i*Ci/(1+r)i + n*M/(1+r)n] / [∑in-1  Ci/(1+r)i + M/(1+r)n]

где,

• C = купонный платеж за период
• M = Номинальная или номинальная стоимость
• r = Эффективная периодическая процентная ставка
• n = количество периодов до погашения

Кроме того, знаменатель, представляющий собой сумму дисконтированного притока денежных средств по облигации, эквивалентен приведенной стоимости или цене облигации. Таким образом, формула для продолжительности может быть дополнительно упрощена, как показано ниже:

Объяснение формулы длительности

Уравнение длительности можно рассчитать, выполнив следующие шаги:

1. Во-первых, вычисляется номинальная или номинальная стоимость выпуска облигаций, и она обозначается буквой М.

2. Теперь купонная выплата по облигации рассчитывается на основе эффективной периодической процентной ставки. Затем также определяется периодичность выплаты купона. Купонный платеж обозначается буквой C, а эффективная периодическая процентная ставка обозначается буквой r.

3. Теперь общее количество периодов до погашения рассчитывается путем умножения количества лет до погашения и частоты купонных выплат в году. Количество периодов до погашения обозначается n. Также отмечается время периодического платежа, которое обозначается i.

4. Наконец, на основе доступной информации уравнение для продолжительности может быть получено следующим образом:

   

Примеры формулы продолжительности (с шаблоном Excel)

Давайте рассмотрим некоторые простые и сложные типы продолжительности. Типы продолжительности. Продолжительность — это мера риска, используемая участниками рынка для измерения чувствительности долгового инструмента, например, облигации, к процентной ставке. Он показывает, насколько чувствительна облигация к изменению процентных ставок. Эту меру можно использовать для сравнения чувствительности облигаций с разным сроком погашения. Есть три разных способа получить показатели длительности, а именно. Продолжительность Маколея, модифицированная продолжительность и эффективная продолжительность. Узнайте больше о формуле, чтобы лучше понять ее.
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%}

Вы можете скачать этот шаблон Excel формулы продолжительности здесь – Формула продолжительности Excel Шаблон

Формула формулы продолжительности – Пример №1

Возьмем пример облигации с ежегодными купонными выплатами. Предположим, что компания XYZ Ltd выпустила облигацию номинальной стоимостью 100 000 долларов США с годовой купонной ставкой 7% и сроком погашения 5 лет. Преобладающая рыночная процентная ставка составляет 10%.

Дано, M = 100 000 долларов.

• С = 7% * 100 000 долларов = 7 000 долларов.
• п = 5
• г = 10%

Знаменатель или цена облигации рассчитывается по формуле:

• Цена облигации = 84 281,19

Расчет числителя формулы Duration выглядит следующим образом:

= (6 363,64 + 11 570,25 + 15 777,61 + 19 124,38 + 310 460,70)

= 363 296,50

Следовательно, расчет дюрации облигации будет следующим:

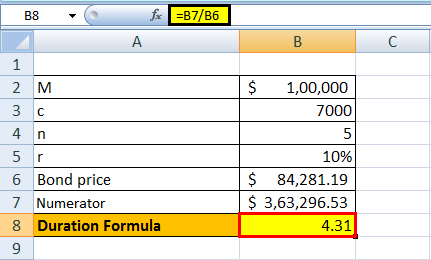
Продолжительность = 363 296,50 / 84 281,19

• Продолжительность = 4,31 года

Формула формулы продолжительности – Пример №2

Возьмем пример облигации с ежегодными купонными выплатами. Предположим, что компания XYZ Ltd выпустила облигацию номинальной стоимостью 100 000 долларов США со сроком погашения 4 года. Преобладающая рыночная процентная ставка составляет 10%. Рассчитайте дюрацию облигации для следующей годовой купонной ставки: (a) 8% (b) 6% (c) 4%

Дано, M = 100 000 долларов.

• п = 4
• г = 10%

Расчет купонной ставки 8%

Купонный платеж (C) = 8% * 100 000 долларов США = 8 000 долларов США.

Знаменатель или цена облигации рассчитывается по формуле:

• Цена облигации = 88 196,16

Расчет числителя формулы Duration будет следующим:

= 311 732,81

Следовательно, расчет дюрации облигации будет следующим:

Продолжительность = 311 732,81/88 196,16

• Продолжительность = 3,53 года

Расчет купонной ставки 6%

Купонный платеж (C) = 6% * 100 000 долларов США = 6 000 долларов США.

Знаменатель или цена облигации рассчитывается по формуле:

• Цена облигации = 83 222,46

Расчет числителя формулы Duration будет следующим:

= 302 100,95

Следовательно, расчет дюрации облигации будет следующим:

Продолжительность = 302 100,95 / 83 222,46

• Продолжительность = 63 года

Расчет купонной ставки 4%

Выплата купона = 4% * 100 000 долларов США = 4 000 долларов США.

Знаменатель или цена облигацииЦена облигацииФормула оценки облигации рассчитывает текущую стоимость вероятных будущих денежных потоков, которые включают купонные платежи и номинальную стоимость, которая является суммой погашения при наступлении срока погашения. Доходность к погашению (YTM) относится к процентной ставке, используемой для дисконтирования будущих денежных потоков. Подробнее рассчитывается по формуле:

• Цена облигации = 78 248,75

Расчет числителя формулы Duration будет следующим:

= 292 469,09

Следовательно, расчет дюрации облигации будет следующим:

Формула продолжительности = 292 469,09 / 78 248,75

• Продолжительность = 3,74 года

Из примера видно, что дюрация облигации увеличивается с уменьшением купонной ставки.

Релевантность и использование формулы продолжительности

Важно понимать концепцию дюрации, поскольку инвесторы в облигации используют ее для проверки чувствительности облигации к изменениям процентных ставок. Срок действия облигации в основном указывает, насколько рыночная цена Рыночная ценаРыночная цена относится к текущей цене, преобладающей на рынке, по которой товары, услуги или активы покупаются или продаются. Ценовая точка, при которой предложение товара соответствует его спросу на рынке, становится его рыночной ценой. Подробнее об облигации изменится из-за изменения процентной ставки. Следует помнить, что процентная ставка и цена облигации движутся в противоположных направлениях, и поэтому цена облигации растет, когда процентная ставка падает, и наоборот.

В случае, если инвесторы ищут выгоды от снижения процентной ставки, инвесторы будут намереваться покупать облигации с большей дюрацией, что возможно в случае облигаций с более низкой купонной выплатой и длительным сроком погашения. С другой стороны, инвесторы, которые хотят избежать волатильности процентной ставки, должны будут инвестировать в облигации с меньшей дюрацией или коротким сроком погашения и более высокой купонной выплатой.

Рекомендуемые статьи

Это было руководство по формуле продолжительности. Здесь мы обсуждаем, как рассчитать продолжительность облигации, используя практические примеры и загружаемый шаблон Excel. Вы можете узнать больше о финансовом анализе из следующих статей –

• Что такое формула ставки купона?Что такое формула ставки купона?Ставка купона, также известная как купонная выплата, представляет собой сумму процентов, которую платят эмитенты облигаций, исходя из номинальной (или номинальной) стоимости облигации и выражается в процентах. Вы можете рассчитать его по следующей формуле: Ставка купона = (Общая сумма годового купонного платежа/Номинальная стоимость облигации) *100Подробнее
• Субординированный долг Значение
• Расчет формулы ценообразования облигаций
• Примеры текущей доходности облигацииПримеры текущей доходности облигации Формула текущей доходности по существу рассчитывает доходность облигации на основе рыночной цены, а не номинальной стоимости. Текущая доходность облигации = Годовая выплата купона / Текущая рыночная ценаПодробнее