Диаграмма Венна

Что такое Диаграмма Венна?

Диаграммы Венна относятся к схематическому представлению множеств с помощью кругов. Этот метод был представлен английским логиком Джоном Венном в 1880 году. Он также известен как диаграммы множеств или логические диаграммы и используется в таких дисциплинах, как математика, статистика и бизнес-исследования.

Эта концепция отражает влияние теории множеств. Набор — это набор различных вещей или объектов или предметов; например, он может содержать числа, символы или фигуры. Теория множеств фокусируется на свойствах совокупности объектов. Он имеет дело с формулами теории множеств, отношениями, операциями и т. Д.

Оглавление

• Что такое Диаграмма Венна?
  • Объяснение диаграммы Венна
  • Формула с расчетом
  • Символы диаграммы Венна
    • Союз (У):
    • Пересечение (∩):
    • Дополнение: (Ас)
  • Приложения
  • Часто задаваемые вопросы (FAQ)
  • Рекомендуемые статьи

Ключевые выводы

• Диаграммы Венна, основанные на теории множеств, относятся к схематическому представлению множеств с помощью кругов. Английский логик Джон Венн ввел его в 1880 году.
• Он имеет широкий спектр применения в академическом и деловом мире. Например, он широко используется в математике, статистике, информатике и дисциплинах управления бизнесом.
• Общие используемые символы: U (объединение), ⋂ (пересечение) и Ac (дополнение A).
• Основная формула для диаграммы, содержащей два набора:

n(AUB) = n(A) + n(B) – n (A ⋂ B)

Объяснение диаграммы Венна

Диаграмма Венна представляет различные наборы, рассматриваемые для изучения или сравнения, с помощью кружков. Круглая область представляет набор. Если между круговыми областями нет перекрытия, представленные множества не имеют ничего общего, а если круговая область перекрывается, между перекрывающимися множествами есть что-то общее. Кроме того, если набор является подмножеством другого набора, меньший круг будет виден внутри другого круга.

Метод может содержать любое количество кругов. Однако сложность схематического представления возрастает с увеличением количества кругов. Так, наиболее распространенным является использование двух или трех кругов. Каждый регион в представлении имеет свое значение, передавая определенную информацию. Как правило, перекрывающаяся или пересекающаяся область выделена графически, чтобы обозначить общность. Диаграмму Венна построить несложно; используя онлайн-шаблоны диаграмм Венна, Майкрософт офис инструменты или онлайн-конструктор диаграмм Венна.

Она очень похожа на диаграмму Эйлера, и определить разницу между ними непросто. Основное отличие состоит в том, что диаграммы Эйлера представляют только существующие отношения; не будет пустых перекрестков. Напротив, диаграмма Венна показывает все возможные логические отношения и представляет пересечения, даже если она пуста.

Формула с расчетом

Основная формула диаграммы Венна:

n(AUB) = n(A) + n(B) – n (A ⋂ B)

Здесь,

• n(AUB): все элементы множеств A и B
• n (A): количество элементов, присутствующих в наборе A.
• n(B): количество элементов, присутствующих в наборе B.
• n (A ⋂ B): количество элементов, общих как в A, так и в B.

Давайте рассмотрим следующий пример диаграммы ВеннаПример диаграммы ВеннаДиаграмма Венна — это один из видов диаграмм в Excel, который используется для анализа отношений, представленных между двумя или более группами через пересекающиеся части кругов. Чтобы лучше понять концепцию, читайте больше.

В отделе продаж и маркетинга компании работает 200 сотрудников, 140 сотрудников участвуют в продажах, а 120 сотрудников участвуют в маркетинговых мероприятиях. Сколько сотрудников принимают участие как в продажах, так и в маркетинге? Также найдите сотрудников, занимающихся только продажами.

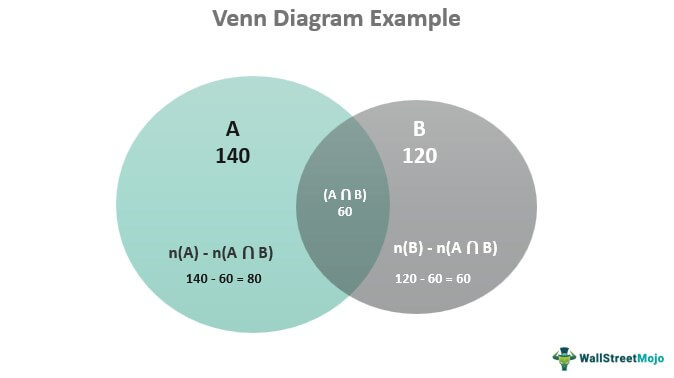
Набор A: Сотрудники, участвующие в продажах

Набор B: Сотрудники, участвующие в маркетинговой деятельности

п(АУБ)= 200

п(А) = 140

п(В) = 120

n(A ⋂ B) — количество сотрудников, участвующих как в продажах, так и в маркетинге. Следовательно, применение формулы дает следующее:

n(A ⋂ B) = n(A) + n(B) – n(AUB)

п(А ⋂ В) = 140 + 120 – 200

= 60

Сотрудники, занимающиеся только продажами = Сотрудники, занимающиеся продажами – Сотрудники, занимающиеся как продажами, так и маркетингом

= п (А) – п (А ⋂ В)

= 140 – 60

= 80

Следовательно, количество сотрудников, участвующих как в продажах, так и в маркетинге, составляет 60 человек, а количество сотрудников, занимающихся только продажами, составляет 80 человек.

Символы диаграммы Венна

Наиболее часто используются следующие символы:

Союз (U):

Он представляет собой объединение всех множеств, представленных на диаграмме Венна. Так, например, если есть два набора, A и B, это будет (AUB).

Пересечение (∩):

Он представляет общие элементы всех присутствующих наборов. Так, например, если есть два множества A и B, это будет (A ⋂ B).

Дополнение: (Ас)

Он представляет то, чего нет в указанном наборе. Ac исключает элемент множества A. Уравнение Ac = U/A изображает дополнение A, где U — универсальное множество, A — подмножество U, а дополнение множества A — все элементы U, которые не являются в.

Приложения

• Он используется в математике и других предметах, чтобы легко проиллюстрировать сложные проблемы или сценарии. Например, при правильном использовании диаграммы Венна избавляют экспертов от необходимости получать ответ, используя сложные шаги и формулы, особенно для ответов в цифрах и значениях. Это также упрощает представление факторов и сценариев, которые трудно объяснить словесно или математически.

• Он используется в бизнес-презентациях для отображения различных бизнес-концепций, визуализации идей и сравнения конкурентов. Например, это помогает обозначить сходства и различия между различными продуктами и прототипами.

Часто задаваемые вопросы (FAQ)

Что такое диаграмма Венна?

Он обычно используется в математике, статистике, информатике, управлении бизнесом и т. д. для представления сложных сценариев или концепций. Метод, основанный на теории множеств, представляет конкретные множества с помощью окружностей. Перекрывающиеся кружки указывают на общность между обозначаемыми ими множествами. Отсутствие перекрытия или пересечения подразумевает отсутствие логической связи между множествами.

Что такое диаграмма Венна A ∩ B?

«∩» — это символ, используемый для обозначения операции пересечения. Например, если диаграмма состоит из двух кругов, представляющих два набора, A и B, то A ∩ B (пересечение A B) указывает на элементы, общие для обоих наборов, представленные перекрывающимся участком двух кругов. В то же время, если есть три множества, A, B и C, пересечение будет A ∩ B ∩ C.

Всегда ли диаграмма Венна состоит из трех кругов?

Нет, теоретически он может содержать любое количество кругов. Однако по мере увеличения количества кругов возрастает и сложность. Следовательно, большинство представлений содержат два или три круга.

Рекомендуемые статьи

Это руководство к тому, что такое диаграмма Венна. Мы объясняем его пример, символы, формулу, приложения и то, как это сделать, используя такие параметры, как шаблоны. Вы можете узнать больше из следующих статей –

• Описательная статистика
• Статистика
• Рассеивание