Т-тест

Т-тест Значение

Т-критерий является окончательной статистической мерой для определения различий между двумя средними значениями, которые могут быть связаны или не связаны. В тестировании используются случайно выбранные образцы из двух категорий или групп. Это статистический метод, в котором образцы выбираются случайным образом, и нет идеального нормального распределения.

Искусственный интеллект поможет тебе заработать!

Подписывайся на канал "Виртуальный Каппер" и получай точные и бесплатные прогнозы на спорт от искусственного интеллекта.

Тип проводимого Т-теста определяется тем, относятся ли анализируемые образцы к одной категории или к разным категориям. Вывод, полученный в процессе, указывает на вероятность того, что средние различия произошли случайно. Тест полезен при сравнении возраста популяции, длины посевов двух разных видов, оценок учащихся и т. д.

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

Оглавление

Т-тест Значение

Т-тест — это статистический метод сравнения средних значений или пропорций двух выборок, собранных либо из одной группы, либо из разных категорий.
Он направлен на проверку гипотезы, которая используется для проверки гипотезы, относящейся к данной совокупности.
Это разница между средними значениями населения и гипотетическим значением.
Одновыборочные, двухвыборочные, парные, равные и неравные дисперсии — это типы Т-тестов, которые пользователи могут использовать для сравнения средних значений.

Объяснение Т-теста

T-тест изучает набор данных, собранных из двух похожих или разных групп, чтобы определить вероятность отличия результата от того, что обычно получается. Точность теста зависит от различных факторов, включая используемые модели распределения и варианты, влияющие на собранные образцы. В зависимости от параметров проводится тест, и в качестве статистического вывода о вероятности того, что обычный результирующий результат обусловлен случайностью, получается Т-значение.

Например, если кто-то хочет выяснить, одинаково ли среднее значение длины лепестков цветка, принадлежащего к двум разным видам, можно провести Т-тест. Пользователь может случайным образом выбрать лепестки двух других видов этого цветка и прийти к стандартному выводу. Финал Интерпретация Т-теста можно получить одним из двух способов:

Нулевая гипотезаНулевая гипотезаНулевая гипотеза предполагает, что выборочные данные и данные населения не имеют различий, или, говоря простыми словами, оно предполагает, что утверждение, сделанное человеком в отношении данных или населения, является абсолютной истиной и всегда верно. Таким образом, даже если выборка берется из населения, результат, полученный в результате изучения выборки, будет таким же, как и предположение. Читать далее означает, что разница между средними равна нулю и где оба средних показаны равными.
Альтернативная гипотеза подразумевает, что разница между средними значениями отлична от нуля. Эта гипотеза отвергает нулевую гипотезу, указывая на то, что набор данных достаточно точен и не случаен.

Однако этот Т-критерий действителен, и его следует проводить только тогда, когда необходимо сравнить среднее или среднее значение только двух категорий или групп. Как только количество сравнений, которые необходимо сделать, больше двух, проводить это не рекомендуется.

Предположения

Тест выполняется на основе набора предположений, которые заключаются в следующем:

Шкала измерения, используемая для такой проверки гипотез Проверка гипотез Проверка гипотез является статистическим инструментом, который помогает измерить вероятность правильности результата гипотезы, полученного после выполнения гипотезы на выборочных данных. Он подтверждает правильность полученных результатов первичной гипотезы. Далее следует набор непрерывных или порядковых шаблонов. Учетные параметры и варианты, влияющие на выборки и окружающие группы, основаны на стандартном рассмотрении.
Тесты полностью основаны на случайной выборке. Поскольку в образцах не сохраняется индивидуальность, их надежность часто подвергается сомнению.
Когда данные наносятся на график по отношению к распределению Т-критерия, они должны следовать нормальному распределению. ареал распространения находится в середине, а немногие — в хвостах, на крайних точках. Это распределение имеет два ключевых параметра: среднее значение (µ) и стандартное отклонение (σ), которые играют ключевую роль в расчете доходности активов и в стратегии управления рисками. Узнайте больше и получите график с колоколообразной кривой.
Для более ясной кривой колокола график колоколообразной кривой изображает нормальное распределение, которое является типом непрерывной вероятности. Он получил свое название из-за формы графика, напоминающего колокол. подробнее, размер выборкиРазмер выборкиФормула размера выборки отражает соответствующий диапазон генеральной совокупности, в которой проводится эксперимент или опрос. Он измеряется с использованием размера совокупности, критического значения нормального распределения при требуемом уровне достоверности, доли выборки и предела погрешности.
Дисперсия должна быть такой, чтобы стандартное отклонение Стандартное отклонение Стандартное отклонение (SD) было популярным статистическим инструментом, представленным греческой буквой «σ», для измерения вариации или дисперсии набора значений данных относительно его среднего (среднего), таким образом интерпретируя достоверность данных. Подробнее выборки практически равны.

Типы

Некоторые из широко используемых Типы Т-тестов следующие:

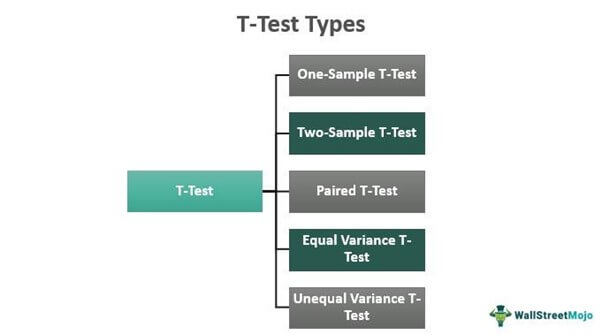
# 1 – Одновыборочный Т-тест

При выполнении этого теста среднее или среднее значение одной группы сравнивается с установленным средним значением, которое является либо теоретическим значением, либо средним значением для населения. Например, учитель хочет определить средний рост учеников 5-го класса и сравнить его с установленным значением более 45 кг.

Учитель сначала случайным образом выбирает группу учеников и записывает индивидуальные веса для достижения этой цели. Затем она узнает средний вес для этой группы и проверяет, соответствует ли он стандартному установленному значению 45+. Формула, используемая для получения результатов одновыборочного t-критерия:

Где,

T = t-статистика
m = среднее значение группы
= теоретическое среднее значение населения
s = стандартное отклонение группы
n = размер выборки

# 2 – Независимый Т-тест с двумя выборками

Это тест, проводимый при изучении и сравнении образцов из двух разных групп, видов или популяций. Он также известен как независимый Т-тест. Например, если учитель хочет сравнить рост учащихся мужского и женского пола в классе 5, она может использовать независимый тест с двумя выборками.

Формула Т-теста используется для расчета это:

Где,

mA – mB = средние значения образцов из двух разных групп или популяций.
nA – nB = соответствующие размеры выборки
s2 = стандартное отклонение или общая дисперсия двух выборок

# 3 – Парный образец Т-теста

Эта проверка гипотезы проводится, когда две группы принадлежат к одной и той же популяции или группе. Группы изучаются либо в два разных времени, либо в двух различных условиях. Формула, используемая для получения t-значения:

Где,

T = t-статистика
m = среднее значение группы
= теоретическое среднее значение населения
s = стандартное отклонение группы
n = размер выборки

# 4 – Т-тест равной дисперсии

Этот тест проводится, когда размер выборки в каждой группе или совокупности одинаков или дисперсия двух наборов данных аналогична. Его также называют объединенным Т-тестом. Применяемая здесь формула выглядит следующим образом:

Где,

Среднее1 и среднее2 = среднее значение каждого набора образцов
var1 и var2 = дисперсия каждого набора образцов
n1 и n2 = количество записей в каждом наборе

# 5 – Т-тест с неравной дисперсией

Проверка неравной дисперсии используется, когда дисперсия и количество выборок в каждой группе различны. Его часто называют тестом Уэлча, а формула такова:

Где,

среднее1 и среднее2 = среднее значение каждого набора образцов
var1 и var2 = дисперсия каждого набора образцов
n1 и n2 = количество записей в каждом наборе

Пример с расчетом

Рассмотрим баллы по каждому предмету на экзамене, проводимом в два этапа.

ПредметОтмечает Фазу 1Отмечает Фазу 2Математика4562Физика4555Химия4555Биология5065История5568География8070

Шаг 1: Вычтите оценки, полученные на обоих этапах.

Шаг 2: Сложите все различия, т.е. -55

Шаг 3: Сократите различия

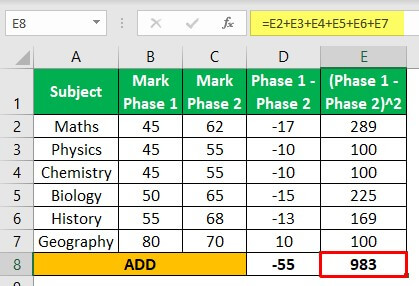
Шаг 4: Сложите все квадраты разности, т. е. 983.

Шаг 5: Использование формулы для расчета значения T

“=” -9,16/√{983-(-55)2/6)}/ (6-1) *6
“=” -9,16/√15,96
“=” -9,16/3,99

Значение T = -2,29

Теперь получите степени свободы. Степени свободы. Степени свободы (df) относятся к числу независимых значений (переменных) в выборке данных, используемой для поиска недостающей части информации (фиксированной) без нарушения каких-либо ограничений, наложенных в динамической системе. Эти номинальные значения могут свободно изменяться, что облегчает пользователям поиск неизвестного или отсутствующего значения в наборе данных.Подробнее. Чтобы получить это, вычтите 1 из размера выборки (6 – 1 = 5). Следующее, что нужно сделать, это выяснить, что p-valueP-valueP-Value, или значение вероятности, является решающим фактором для нулевой гипотезы для вероятности того, что предполагаемый результат будет истинным, будет принят или отклонен, и принятие альтернативного результата в случае отклонения предполагаемых результатов. читать больше, что, если оно меньше по значению, подтверждает результат нулевой гипотезы. Например, если p-значение составляет около 0,9, т. е. 90%, это указывает на то, что полученное T-значение, вероятно, является случайным наблюдением. С другой стороны, если p-значение составляет около 0,025, т. е. 2,5%, полученный результат или t-значение является значимым.

Часто задаваемые вопросы (FAQ)

Что такое Т-тест?

T-критерий измеряет разницу между двумя средними значениями, которые могут быть связаны или не быть связаны друг с другом, указывая на вероятность того, что различия произошли случайно. Точность полученных значений зависит от различных факторов, в том числе от используемых закономерностей распределения и вариантов, влияющих на собранные образцы.

Когда используется Т-тест?

Т-тест действителен только тогда, когда необходимо сравнить средние значения только двух категорий или групп. Как только количество сравнений, которые необходимо сделать, больше двух, проводить этот тест не рекомендуется.

• Одна выборка используется для определения среднего или среднего значения одной группы, чтобы сравнить его с установленным средним значением.
• Независимый двухвыборочный тест проводится, когда изучаются и сравниваются образцы из двух разных групп, видов или популяций.
• Парная выборка — это проверка гипотез, проводимая, когда две группы принадлежат к одной и той же совокупности или группе.
• Равная дисперсия проводится, когда размер выборки в каждой группе или генеральной совокупности одинаков или дисперсия двух наборов данных аналогична.
• Неравная дисперсия используется, когда дисперсия и количество выборок в каждой группе различаются.

Что такое T-тесты и значения P?

В то время как значения T указывают на вероятность того, что разница между средними значениями выборки является результатом, полученным случайно, значения p отражают вероятность наличия достаточных доказательств, чтобы свести на нет безразличие между средним значением двух выборок.

Т-тест

Т-тест Значение

Искусственный интеллект поможет тебе заработать!