Статистическая значимость

Определение статистической значимости

Статистическая значимость – это вероятность того, что наблюдение не вызвано ошибкой выборки. Это подразумевает, что наблюдение имеет определенную причину. Следовательно, чтобы считать наблюдение статистически значимым, оно должно пройти тестирование.

Чтобы доказать статистическую значимость, набор данных должен отклонить нулевую гипотезу. Нулевая гипотеза. абсолютная истина и всегда прав. Таким образом, даже если выборка будет взята из генеральной совокупности, результат, полученный при изучении выборки, будет таким же, как и предположение. Читать далее. Чтобы доказать ошибочность нулевой гипотезы, p-значение наблюдения должно быть меньше уровня значимости. p-valueP-valueP-Value, или значение вероятности, является решающим фактором для нулевой гипотезы для вероятности того, что предполагаемый результат окажется истинным, будет принят или отклонен, и принятия альтернативного результата в случае отклонения предполагаемых результатов. . Читать дальше — это вероятность того, что наблюдение вызвано случайными факторами.

Оглавление

• Определение статистической значимости
  • Понимание уровней статистической значимости
  • Тест статистической значимости (P-значение)
    • #1 – Статистическая проверка гипотез
    • # 2 – Статистически значимое значение p
  • Расчет статистической значимости
  • Статистическая и практическая значимость
  • Часто задаваемые вопросы (FAQ)
  • Рекомендуемые статьи

Ключевые выводы

• Статистическая значимость показывает, что наблюдение вызвано конкретной причиной, а не случайным фактором.
• Уровень значимости представлен α. Исследователь устанавливает его значения и обычно составляет 0,01, 0,05 или 0,1.
• Нулевая гипотеза предполагает, что исследование ложно. Однако альтернативная гипотеза, являющаяся предположением исследователя, может оказаться верной, отвергнув нулевую гипотезу.
• Условное значение α = 0,05. Следовательно, если значение p для набора данных ≤ 0,05, то результат статистически значим. Если p-значение > 0,05, то исследование может быть статистически незначимым.

Понимание уровней статистической значимости

Статистическая значимость широко применяется исследователями в качестве инструмента количественного исследования для принятия решений. Этот инструмент применяется в различных областях, таких как бизнес, маркетинг, реклама, инвестиции и финансы.

Следующие два фактора определяют значимость.

1. Размер образца: Количество наблюдений в огромной степени влияет на уровень значимости. Большой набор данных (обязательно рандомизированная выборка) часто устраняет ошибку выборкиОшибка выборкиФормула ошибки выборки используется для расчета статистической ошибки, которая возникает, когда человек, проводящий тест, не выбирает выборку, которая представляет всю рассматриваемую совокупность. Формула для ошибки выборки = Z x (σ /√n)подробнее.
2. Размер эффекта: Корреляция между двумя наборами данных или переменными называется размером эффекта. Больший эффект sizeEffect SizeEffect size измеряет интенсивность взаимосвязи между двумя наборами переменных или групп. Он рассчитывается путем деления разницы между средними значениями, относящимися к двум группам, на стандартное отклонение. Это статистическая концепция. Следовательно, она подразумевает, что два разных исследования показывают очень похожие значения. Больший размер эффекта указывает на то, что данные статистически более значимы.

Значение альфа (α) представляет собой статистическую значимость. Традиционное значение альфы составляет 0,05, что составляет 5%. Он служит 95% порогом значимости. Это означает, что вероятность точности результата составляет 95%.

Для достижения статистической значимости должно выполняться хотя бы одно из заданных условий:

1. Значение p должно быть ниже значения альфа.
2. Значения нулевой гипотезы не должны иметь места в доверительном интервале.

Доверительный интервал Доверительный интервал Доверительный интервал относится к степени неопределенности, связанной с конкретной статистикой, и часто используется вместе с пределом погрешности. Доверительный интервал = среднее значение выборки ± критический фактор × стандартное отклонение выборки. read more относится к гарантированному диапазону, в который попадают фактические значения. Для p-значения 0,05, то есть 5%, оставшиеся 95% считаются доверительным интервалом.

Например, в июне 2020 г. ОСИНА Испытание не достигло статистической значимости по своей основной конечной точке. Об этом сообщило агентство Рейтер.

Тест статистической значимости (P-значение)

Статистическая значимость включает в себя нахождение результата и его проверку. Набор данных должен успешно отвергнуть нулевую гипотезу.

#1 – Статистическая проверка гипотез

Гипотеза – это предположение исследователя. Исследователи предполагают, что они получат тот или иной результат еще до проведения теста. Это предположение основано на взаимосвязи между различными переменными или наборами данных.

Два типа гипотез, используемых для анализа данных, следующие:

1. Нулевая гипотеза: Теперь, если теория, предложенная исследователями, неверна, гипотеза исследователя считается недействительной. Это обозначается H0.
2. Альтернативная гипотеза: Однако, если теория исследователя оказывается верной, она называется альтернативной гипотезой. Обозначается H1.

# 2 – Статистически значимое значение p

Значение p обозначает значение вероятности, то есть вероятность результата, являющегося результатом случайности или совпадения, а не фактов. Таким образом, уровень статистической значимости можно анализировать с помощью p-значения, которое находится в диапазоне от 0 до 1. Статистический результат считается точным, когда p-значение равно или меньше 0,05. Другими словами, вероятность того, что данные были получены случайно или случайно, составляет всего 5%.

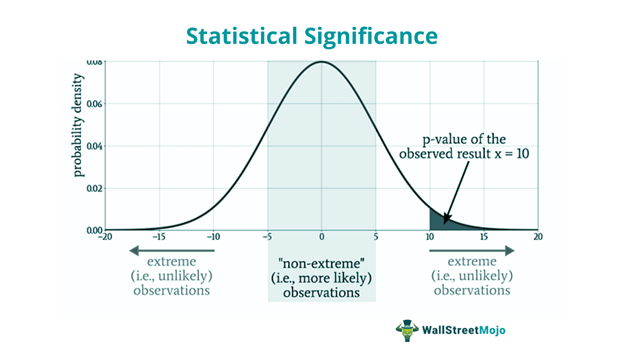
Таким образом, тестирование приведет к следующим двум возможностям.

• p-значение ≤ 0,05: значение p, равное или меньшее 0,05, указывает на то, что нулевая гипотеза, вероятно, ложна. Таким образом, есть шансы, что результат будет более статистически значимым.
• р-значение > 0,05: Напротив, значение, превышающее 0,05, означает, что нулевая гипотеза кажется вероятной, и результат может быть статистически незначимым.

Расчет статистической значимости

Рассмотрим следующую задачу на основе гипотетического сценария. Самуэль, владелец парка развлечений, хочет, чтобы гости проводили больше времени в парке. Среднее время, проведенное 20 посетителями парка, составляет 199 минут. Сэмюэл решает установить новые аттракционы. Для теста порог значимости принят равным 5%, среднее значение выборки равно 200 минутам, а стандартное отклонение равно 200 минутам. На основе полученных данных проведите тест значимости для Сэмюэля.

Данные:

• µ = 199 минут
• п = 20
• µ остается 199 минут до установки новых аттракционов
• µ > 199 минут после установки новых аттракционов
• α = 5% или 0,05
• х = 200 минут
• σ = 200 минут

Расчет

Мы будем применять z-тест здесь,

Z = (x̄ – μ) / √ (σ2 / n)

Z = (200 – 199) / √(200 / 20)

Z = 1/3,16228

Z = 0,31623 = 0,3

Теперь давайте определим z-оценку или p-значение для данной z-таблицы:

Z0,000,10,20,30,40,00,500000,503990,507980,511970,51595

Таким образом, p-значение равно 0,51197.

Здесь, p-значение > α, т.е.., 0,51197 > 0,05

Следовательно, нулевая гипотеза может быть верной, и результат не является статистически значимым.

В качестве альтернативы пользователи могут выбирать из различных онлайн-калькуляторов для проведения тестов значимости.

Статистическая и практическая значимость

Статистическая значимость исключает случайное совпадение и указывает на то, что данные являются результатом определенной причины. Однако практическая значимость обнаруживает величину этого эффекта и его актуальность в реальном мире.

В то время как исследователи используют размер выборки и p-значение для установления статистической значимости, размер эффекта наборов данных указывает на практическую значимость.

Таким образом, получение статистической значимости без определения практической значимости было бы не очень полезным.

Часто задаваемые вопросы (FAQ)

Что такое статистическая значимость в исследованиях?

Тесты значимости широко используются в научных, экономических и медицинских исследованиях для определения надежности результатов тестов путем анализа шансов на истинность нулевой гипотезы.

Как определить статистическую значимость?

Шаги для расчета значимости следующие.
1. Найдите нулевую и альтернативную гипотезы, т. е. H0 и H1.
2. Предположим порог значимости или уровень значимости (α).
3. Получите образец и данные для проведения теста.
4. Запустите статистические тесты, такие как z-тест, T-тест, ANOVA или Chi-Square.
5. Проверьте, являются ли данные статистически значимыми, определив p-значение.
6. Интерпретируйте результат или завершите исследование.

Почему значимо значение p, равное 0,05?

Значение p, равное 0,05, представляет собой альфа, т.е. порог статистической значимости. Это граница вероятности, поэтому любое значение, выходящее за ее пределы, считается статистически незначимым. Если p-значение превышает 5%, это указывает на то, что более 5% значений вызваны случайностью. В результате набор данных нельзя использовать в качестве существенного доказательства причинно-следственной связи.

Рекомендуемые статьи

Это было Руководство по статистической значимости и ее значению. Здесь мы обсуждаем тесты значимости (значение p) и то, как понять его уровни, а также примеры и расчеты. Вы также можете ознакомиться со следующими статьями, чтобы узнать больше:

• Проверка гипотезы
• Степени свободы
• Тест хи-квадрат в Excel