Среднеквадратичное отклонение

Определение стандартного отклонения

Стандартное отклонение измеряет величину вариации или дисперсии в наборе значений данных относительно его среднего значения (среднего). Это статистический инструмент, используемый для интерпретации надежности данных. Он представлен символом «σ».

Если отклонение меньше, точки данных близки к среднему значению, и данные считаются
надежный. Напротив, если отклонение велико, точки данных разбросаны дальше от среднего значения; такие данные считаются менее надежными. Стандартное отклонение используется при анализе общего риска и доходности портфеля.

Оглавление

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

Определение стандартного отклонения

Стандартное отклонение — это статистический инструмент, который измеряет волатильность данных. Он указывает, в какой степени значения выборки отклоняются от средних значений. Он вычисляется как квадратный корень из дисперсии и обозначается символом «σ» (греческая буква).
σ не может быть отрицательным значением и может быть равен 0 только в том случае, если значения в наборе данных равны и не имеют вариаций.
В финансах этот математический инструмент применяется для определения уровня рисков, связанных с конкретными инвестициями или активами. Метод измеряет спред соответствующих цен и доходов. Более высокое отклонение отражает высокую волатильность и наоборот.
Если символ σ обозначает стандартное отклонение, n — общее количество наблюдений в наборе данных, xi — i-е количество наблюдений, а µ — выборочное среднее, то отклонение вычисляется по следующей формуле:

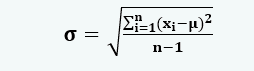
В большинстве случаев минимальное стандартное отклонение считается благоприятным. Если отклонение в предыдущих колебаниях цен для конкретной акции невелико, это считается надежной инвестиционной возможностью.

Этот статистический инструмент помогает исследователям и аналитикам понять распространение данных, чтобы
определить степень разброса данных. Этот математический аппарат показывает
разброс выборочных значений от среднего значения.

Стандартные ошибки подчеркивают точность среднего значения выборки по отношению к генеральной совокупности.
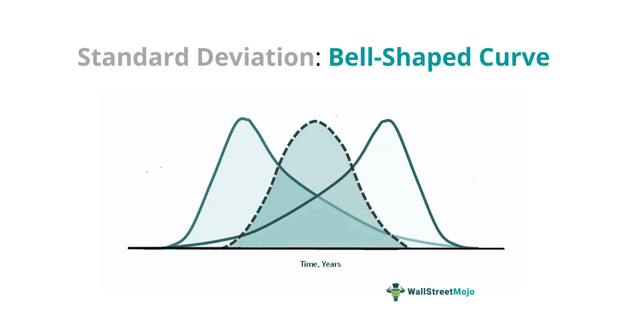
означает, когда данные обширны и широко распространены. На графике отклонение может лежать влево, вправо или в обе стороны — формирование колоколообразной кривойГрафик колоколообразной кривой изображает нормальное распределение, которое является типом непрерывной вероятности. Он получил свое название из-за формы графика, напоминающего колокол. читать далее.

Уравнение стандартного отклонения

Уравнение для определения стандартного отклонения ряда данных выглядит следующим образом:

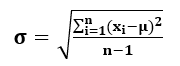
т.е. σ=√v

Также, µ =∑x/n

Здесь,

σ — это символ, обозначающий стандартное отклонение.
n — количество наблюдений в наборе данных.
xi — i-е количество наблюдений в наборе данных.
µ — среднее значение выборки.
V — дисперсия.
∑x — сумма всех значений в наборе данных.

Расчет

Основные шаги, используемые для поиска и расчета стандартного отклонения, следующие:

Сначала определите среднее значение набора данных.
Затем подготовьте диаграмму со значениями выборки и разницей между выборкой.
значения и средние значения.
В следующем столбце найдите квадрат разностей.
Чтобы получить дисперсию, сложите все квадраты и разделите результат на разницу между общим количеством наблюдений и 1.
Наконец, найдите квадратный корень из дисперсии, чтобы получить стандартное отклонение.

Пример

Давайте рассмотрим несколько примеров, чтобы понять практические последствия:

Найти отклонение цен на сырую нефть за год, когда среднемесячные цены за литр были следующими:

МесяцСредняя цена за литр в долларахЯнварь0,83Февраль0,81Март0,78Апрель0,82Май0,79Июнь0,75Июль0,76Август0,79Сентябрь0,81Октябрь0,77Ноябрь0,76Декабрь0,75

Решение:

Расчет среднего:

µ = ∑x/n

µ = 9,42/12

= 0,785 доллара за литр

С. №МесяцСредняя цена за литр в $ (x)х – 0,785 доллара США(х – 0,785 долл. США)21January0.830.0450.0020252February0.810.0250.0006253March0.78-0.0050.0000254April0.820.0350.0012255May0.790.0050.0000256June0.75-0.0350.0012257July0.76-0.0250.0006258August0.790.0050.0000259September0.810.0250.00062510October0.77-0.0150.00022511November0. 76-0.0250.00062512декабрь0.75-0.0350.00122512–9.42 0,0085

Расчет стандартного отклонения :

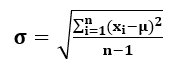
σ = √ [0.0085 / (12-1)]
σ = √ (0,00077272727)
σ = 0,0277979724571285 долл. США

Таким образом, стандартное отклонение цен на нефть за литр для данного года равно
0,0277979724571285.

Интерпретация

Стандартное отклонение указывает на волатильность или дисперсию значений конкретного распределения. Он показывает, в какой степени значения выборки отклоняются от средних значений. Таким образом, эта мера облегчает сравнение и анализ.

Ниже приведены различные интерпретации полученного результата:

Если σ велико, то волатильность анализируемых данных также высока.
Точно так же, когда σ низкое, дисперсия между точками данных также незначительна.
В распределении σ может быть равно 0 только тогда, когда разница между точками данных равна нулю. Это также наименьшее значение отклонения, которое можно получить.
Невозможно получить отрицательное значение σ, так как числитель включает квадрат разности между выборочными значениями и средними значениями.
Кроме того, количество наблюдений всегда больше 1; следовательно, знаменатель должен быть положительным значением.
Стандартное отклонение измеряется в тех же единицах, что и значения распределения. Например, в приведенном выше примере σ выражается в долларах.
Выбросы (чрезвычайно высокие или низкие значения) существенно влияют на измерения отклонения.

Часто задаваемые вопросы (FAQ)

Что такое стандартное отклонение?

Стандартное отклонение — это статистический метод, используемый для нахождения разброса данных в распределении с использованием средних значений. Обозначается символом «σ».

Как рассчитать стандартное отклонение?

Стандартное отклонение рассчитывается как квадратный корень из дисперсии. Дисперсия — это сумма квадрата разности между каждым значением в наборе данных и их средними значениями, деленная на значение, полученное путем вычитания единицы из общего числа наблюдений.

Почему стандартное отклонение важно?

Он определяет степень изменчивости значений в выборочном распределении. Это широко используемый статистический инструмент в финансах, инвестициях и бизнесе для интерпретации величины риска, связанного с ценной бумагой или активом. В большинстве случаев минимальное отклонение считается благоприятным. Если отклонение в предыдущих колебаниях цен для конкретной акции невелико, это считается надежной инвестиционной возможностью.

Может ли стандартное отклонение быть равным нулю?

Единственный случай, когда он может быть равен нулю, — это когда все точки данных в распределении одинаковы. Нулевое отклонение указывает на нулевой разброс или изменчивость значений. Для реальных сценариев это практически невозможно.

Среднеквадратичное отклонение

Определение стандартного отклонения