Среднее геометрическое

Определение среднего геометрического

Среднее геометрическое (GM) — это метод центральной тенденции, который определяет среднее значение мощности данных ряда роста. Он вычисляется как корень n-й степени мультипликативного результата всех цифр данных до n.

Этот метод подходит для определения средней стоимости отдельных инвестиций или портфеля в целом за определенный период времени. Он точно оценивает средние значения, относящиеся к непрерывному ряду взаимозависимых значений.

Оглавление

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

Определение среднего геометрического

Среднее геометрическое (GM) относится к центральной мере тенденции, которая оценивает среднее значение ряда путем умножения всех чисел и последующего нахождения n-го корня произведения.
Это среднее значение мощности, используемое для непрерывного ряда данных с близким распределением взаимозависимых значений или элементов.
Метод GM применяется для расчета пропорционального роста фондовых индексов. Кроме того, он устанавливает среднюю доходность инвестиций или портфелей, которые обеспечивают совокупные выгоды.

Объяснение среднего геометрического

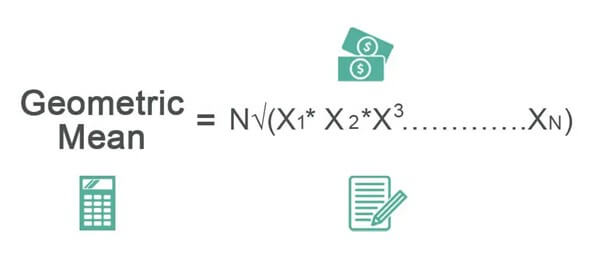
Среднее геометрическое используется с данными временных рядов для определения начисления сложных процентовНачисление сложных процентовНачисление сложных процентов — это метод инвестирования, при котором доход, полученный от инвестиции, реинвестируется, а новая основная сумма увеличивается на сумму реинвестированного дохода. В зависимости от срока вклада к основной сумме прибавляются проценты. читать дальше средний. Данные временных рядов являются кульминацией наблюдений, собранных посредством повторных измерений с течением времени. Когда данные временного ряда представлены на графике, одной из осей всегда будет время.

Этот показатель часто называют средней мощностью. Он в основном используется для сравнения средних показателей роста различных инвестиционных продуктов или портфелей. Он имеет экспоненциальную связь со средним арифметическим. Среднее арифметическое Среднее арифметическое обозначает среднее значение всех наблюдений ряда данных. Это совокупность всех значений в наборе данных, деленная на общее количество наблюдений. Подробнее о логарифмах.

Этот метод нормализует диапазоны, уменьшая влияние доминирующих значений на вес. Таким образом, огромные значения больше не влияют на асимметричные модели распределения. Этот метод дает лучшие результаты, когда переменные сильно искажены.

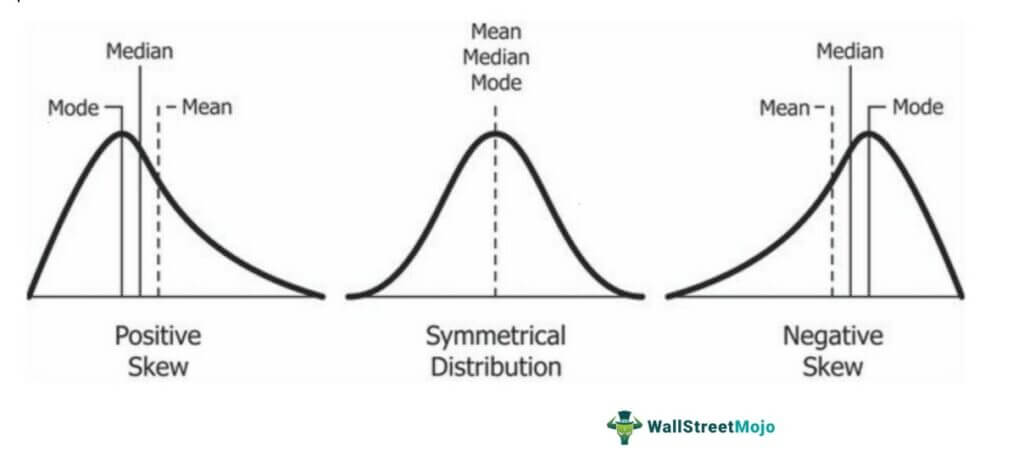
АсимметричностьАсимметрияАсимметрия — это отклонение или степень асимметрии, показанная кривой нормального распределения или нормальным распределением в заданном наборе данных. Если кривая смещается вправо, это считается положительной асимметрией, а кривая, сдвинутая влево, представляет собой отрицательную асимметрию. Подробнее относится к симметрии. Если асимметрия равна 0, данные идеально симметричны. Если нормальное распределение Нормальное распределение Нормальное распределение представляет собой колоколообразную кривую распределения частот, которая помогает описать все возможные значения, которые случайная величина может принимать в заданном диапазоне, при этом большая часть области распределения находится в середине, а небольшая часть — в хвостах, на крайних точках. . Это распределение имеет два ключевых параметра: среднее (µ) и стандартное отклонение (σ), которые играют ключевую роль в расчете доходности активов и в стратегии управления рисками. неравномерно с асимметрией больше нуля или положительной асимметрией. Положительная асимметрия. Положительная асимметрия. распределение – это такое, в котором среднее значение, медиана и мода являются положительными, а не отрицательными или нулевыми. Распределение данных более сконцентрировано на одной стороне шкалы, с длинным хвостом справа. Читать дальше, то его правый хвост будет более продолжительным, чем левый.

Характеристики

Следующие свойства выделяют среднее геометрическое среди других центральных тенденций. :

Даже если каждое значение в ряду данных заменить на GM, их произведение останется прежним.
В конкретном наборе данных среднее геометрическое значение всегда ниже значения его среднего арифметического.
Когда соответствующие наблюдения GM двух рядов данных умножаются, полученное значение равно результату умножения их значений GM.

Формула среднего геометрического

Вычисление среднего геометрического помогает инвесторам установить среднее значение сложных процентов для данного ряда данных. Он оценивается по следующим формулам: