Регрессия методом наименьших квадратов

Определение метода регрессии наименьших квадратов

Метод регрессии наименьших квадратов — это форма регрессионного анализа, которая устанавливает связь между зависимыми и независимыми переменными вдоль линейной линии. Эта линия относится к «линии наилучшего соответствия».

Регрессионный анализ — это статистический метод, с помощью которого можно оценить или предсказать неизвестные значения одной переменной по известным значениям другой переменной. Переменная, используемая для прогнозирования переменной интереса, называется независимой или объясняющей переменной, а прогнозируемая переменная называется зависимой или объясняемой переменной.

Рассмотрим две переменные x и y. Они нанесены на график со значениями x на оси x и y на оси y. Точки представляют эти значения на графике ниже. Через точки проводится прямая линия, называемая линией наилучшего соответствия.

Где,

• ŷ = зависимая переменная
• х = независимая переменная
• a = y-перехват
• b = наклон линии

Наклон линии b можно рассчитать по следующей формуле:

Или

Y-пересечение, ‘a’ рассчитывается по следующей формуле:

Линия наилучшего соответствия в регрессии наименьших квадратов

Линия наилучшего соответствияЛиния наилучшего соответствияЛиния наилучшего соответствия — это математическое понятие, которое связывает точки, разбросанные по графику.Подробнее

представляет собой прямую линию, проведенную через разброс точек данных, которая лучше всего представляет взаимосвязь между ними.

Давайте рассмотрим следующий график, на котором набор данных построен по осям x и y. Эти точки данных представлены синими точками. Через эти точки проведены три линии – зеленая, красная и синяя. Зеленая линия проходит через одну точку, а красная линия проходит через три точки данных. Однако синяя линия проходит через четыре точки данных, а расстояние между остаточными точками и синей линией минимально по сравнению с двумя другими линиями.

На приведенном выше графике синяя линия представляет собой линию наилучшего соответствия, поскольку она находится ближе всего ко всем значениям, а расстояние между точками вне линии до линии минимально (расстояние между остатками до линии наилучшего соответствия — также называются суммами квадратов остатков). Однако в двух других линиях, оранжевой и зеленой, расстояние между остатками и линиями больше, чем у синей линии.

Метод наименьших квадратов обеспечивает наиболее тесную связь между зависимой и независимой переменными. измеряется в математическом, статистическом или финансовом моделировании. Подробнее путем минимизации расстояния между остатками и линией наилучшего соответствия, т. е. сумма квадратов остатков минимальна при таком подходе. Отсюда и термин «наименьшие квадраты».

Примеры линии регрессии методом наименьших квадратов

Применим эти формулы к следующему вопросу:

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel регрессии наименьших квадратов здесь – Шаблон Excel регрессии наименьших квадратов

Пример №1

Подробная информация об опыте работы технических специалистов в компании (в течение нескольких лет) и рейтинге их эффективности приведены в таблице ниже. Используя эти значения, оцените рейтинг производительности для техника с 20-летним стажем.

Опыт работы техническим специалистом (в годах)рейтинг производительности16871288188946837810805751283

Решение –

Чтобы сначала вычислить метод наименьших квадратов, мы вычислим точку пересечения Y (a) и наклон линии (b) следующим образом:

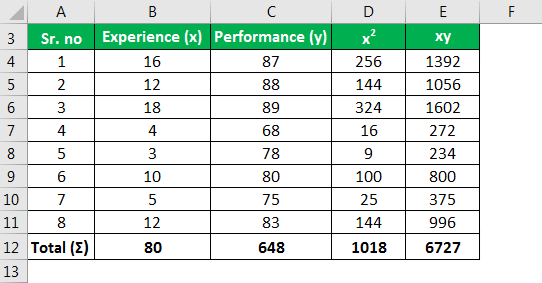
Наклон линии (b)

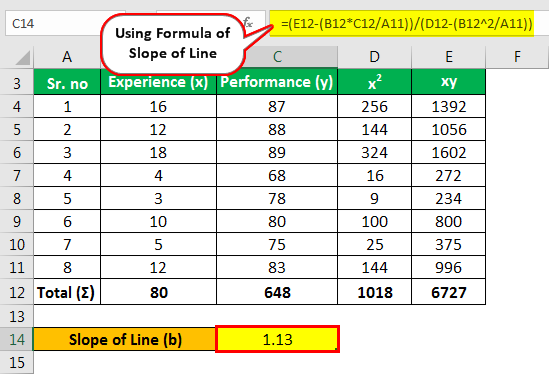
• б = 6727 – [(80*648)/8] / 1018 — [(80)2/8]
• = 247/218
• = 1,13

Y-пересечение (а)

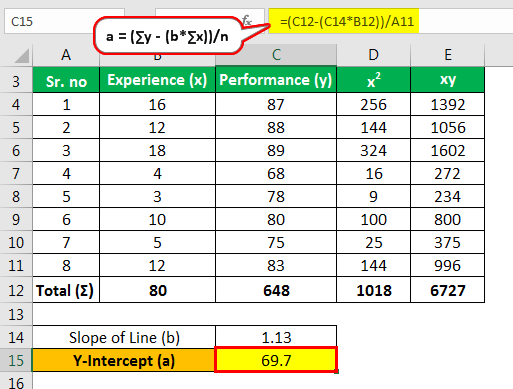
• а = 648 – (1,13)(80)/8
• = 69,7

Линия регрессии рассчитывается следующим образом:

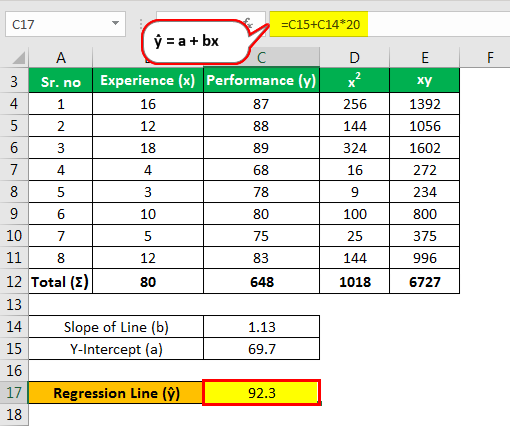
Подставив 20 вместо значения x в формуле,

• ŷ = а + Ьх
• дом = 69,7 + (1,13)(20)
• дом = 92,3

Рейтинг производительности для техника с 20-летним стажем оценивается в 92,3.

Пример #2

Уравнение регрессии наименьших квадратов с использованием Excel

Можно вычислить уравнение регрессии наименьших квадратов с помощью Excel, выполнив следующие шаги:

• Вставка таблицы данных в excelТаблица данных в ExcelТаблица данных в Excel — это тип инструмента анализа «что, если», который позволяет сравнивать переменные и видеть, как они влияют на результат и общие данные. Его можно найти на вкладке данных в разделе анализа «что, если».Подробнее.

• Вставьте точечную диаграмму, используя точки данных.

• Вставьте линию тренда в точечный график.

• В параметрах линии тренда выберите линейную линию тренда и выберите «Отображать уравнение на графике».

• Уравнение регрессии наименьших квадратов для заданного набора данных Excel отображается на диаграмме.

Таким образом, можно рассчитать уравнение регрессии наименьших квадратов для набора данных Excel. Прогнозы и анализ тенденций можно сделать с помощью уравнения. Инструменты Excel также обеспечивают подробные регрессионные вычисления.

Преимущества

• Метод регрессионного анализа наименьших квадратов лучше всего подходит для моделей прогнозирования и анализа тенденций. Лучше всего его можно использовать в экономике, финансах и на фондовых рынках, где значение любой будущей переменной предсказывается с помощью существующих переменных и отношений между ними.
• Метод наименьших квадратов обеспечивает наиболее тесную связь между переменными. Разница между суммами квадратов невязок к линии наилучшего соответствия при этом методе минимальна.
• Механизм расчета прост и удобен в применении.

Недостатки

• Метод наименьших квадратов устанавливает наиболее тесную связь между заданным набором переменных. Механизм вычисления чувствителен к данным, и в случае каких-либо выбросов (исключительных данных) результаты могут существенно повлиять.
• Этот тип расчета лучше всего подходит для линейных моделей. Для нелинейных уравнений применяются более исчерпывающие вычислительные механизмы.

Заключение

Метод наименьших квадратов является одной из самых популярных моделей прогнозирования и анализа тенденций. пытаться принимать наилучшие решения на основе результатов проведенного анализа методов. При правильном расчете он дает наилучшие результаты.

Рекомендуемые статьи

Эта статья представляет собой руководство по методу регрессии наименьших квадратов и его определению. Здесь мы обсуждаем формулу для расчета линии регрессии по методу наименьших квадратов вместе с примерами Excel. Вы можете узнать больше из следующих статей: –

• Примеры линейной регрессии
• Формула множественного регрессионного анализа
• Дисперсионный анализ в Excel
• ЭВМА