Относительное стандартное отклонение

Что такое относительное стандартное отклонение?

Относительное стандартное отклонение (RSD) измеряет отклонение набора чисел, рассеянных вокруг среднего значения. Его можно рассчитать как отношение стандартного отклонения к среднему для набора чисел. Чем больше отклонение, тем дальше цифры от среднего. Чем меньше отклонение, тем ближе числа к среднему.

Оглавление

Что такое относительное стандартное отклонение?

Формула относительного стандартного отклонения

Относительное стандартное отклонение = (стандартное отклонение / среднее значение) * 100

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

Стандартное отклонение σ = √ [Σ(x- μ)2 / N]

Например, на финансовых рынках это соотношение помогает количественно оценить волатильность. Формула RSD помогает оценить риск, связанный с безопасностью движения на рынке. Если это отношение к безопасности высокое, то цены будут разбросаны, и ценовой диапазон будет широким. Это означает, что волатильность ценной бумаги высока. Если коэффициент по безопасности низкий, то и цены будут меньше разбросаны. Это означает, что волатильность ценной бумаги низкая.

Как рассчитать относительное стандартное отклонение? (Шаг за шагом)

Выполните следующие шаги:

Первый, рассчитать среднее значение (µ), т. е. среднее число чисел
Получив среднее значение, вычтите среднее значение из каждого числа, что даст нам отклонение, и возведите отклонения в квадрат.
Добавьте квадраты отклонений и разделите это значение на общее количество значений. Это дисперсия.
Квадратный корень из дисперсии даст нам стандартное отклонение (σ).
Разделите стандартное отклонение на среднее значение и умножьте на 100.
Ура! Вы только что взломали, как рассчитать формулу относительного стандартного отклонения.

Подводя итог, можно сказать, что деление стандартного отклонения на среднее значение и умножение на 100 дает относительное стандартное отклонение. Вот как это просто!

Прежде чем мы двинемся дальше, есть некоторая информация, которую вы должны знать. Во-первых, когда данные представляют собой совокупность сами по себе, приведенная выше формула идеальна, но если данные представляют собой выборку из совокупности (скажем, кусочки из большего набора), расчет изменится.

Изменение формулы выглядит следующим образом:

Стандартное отклонение (выборка) σ = √ [Σ(x- μ)2 / N-1]

Когда данные представляют собой совокупность, их следует разделить на N.

Когда данные представляют собой выборку, их следует разделить на N-1.

Примеры

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel формулы относительного стандартного отклонения здесь – Формула относительного стандартного отклонения Шаблон Excel

Пример №1

Оценки, полученные тремя учащимися за тест, следующие: 98, 64 и 72. Но сначала рассчитайте относительное стандартное отклонение.

Решение:

Ниже приведены данные для расчета

Иметь в виду

Расчет среднего

μ = Σx/n

где м среднее значение; Σxi представляет собой сумму всех значений, и н это количество предметов

мк = (98+64+72) / 3

м= 78

Среднеквадратичное отклонение

Следовательно, расчет стандартного отклонения выглядит следующим образом:

Складываем значения всех (х – м)2 мы получаем 632

Поэтому, Σ(х-м)2 = 632

Расчет стандартного отклонения:

σ = √ [Σ(x- μ)2 / N]

=√632/3

σ = 14.51

РСД

Формула = (стандартное отклонение / среднее значение) * 100

= (14,51/78)*100

Стандартное отклонение будет –

РСД = 78 +/- 18,60%

Пример #2

В следующей таблице показаны цены на акции XYZ. Найдите RSD за 10-дневный период.

Решение:

Ниже приведены данные для расчета относительного стандартного отклонения.

Иметь в виду

Расчет среднего

μ = (53,73+ 54,08+ 54,14+ 53,88+ 53,87+ 53,85+ 54,16+ 54,5+ 54,4+ 54,3) / 10

м = 54.091

Среднеквадратичное отклонение

Следовательно, расчет стандартного отклонения выглядит следующим образом:

Расчет стандартного отклонения:

σ = 0,244027

РСД

Формула = (стандартное отклонение / среднее значение) * 100

= (0,244027/54,091)*100

Стандартное отклонение будет –

РСД = 0,451141

Пример формулы №3

Организация провела медосмотр своих сотрудников и обнаружила, что у большинства сотрудников избыточный вес, вес (в кг) для 8 сотрудников указан ниже, и вам необходимо рассчитать относительное стандартное отклонение.

Решение:

Ниже приведены данные для расчета относительного стандартного отклонения.

Иметь в виду

Расчет среднего

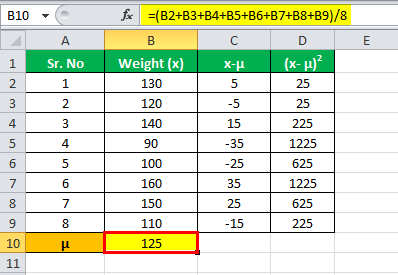
μ = (130 + 120 + 140 + 90 + 100 + 160 + 150 + 110) / 8

м = 125

Среднеквадратичное отклонение

Следовательно, расчет стандартного отклонения выглядит следующим образом:

Расчет стандартного отклонения:

σ = 24.4949

РСД

Формула = (стандартное отклонение / среднее значение) * 100

= (24,49490/125)*100

Стандартное отклонение будет –

РСД = 19,6

Поскольку данные представляют собой выборку из совокупности, необходимо использовать формулу RSD.

Актуальность и использование

Относительное стандартное отклонение помогает измерить дисперсию. В статистике дисперсия (или разброс) является средством описания степени распределения данных вокруг центрального значения или точки. Это помогает понять распределение данных о наборе значений, связанных со средним значением. Это позволяет нам анализировать точность набора значений. Значение RSD выражается в процентах. Это помогает понять, является ли стандартное отклонение маленьким или огромным по сравнению со средним значением для набора значений.

Знаменатель для расчета RSD является абсолютным значением среднего, и он никогда не может быть отрицательным. Следовательно, RSD всегда положителен. Стандартное отклонение анализируется в контексте среднего значения с помощью RSD. RSD используется для анализа волатильности ценных бумаг. Кроме того, RSD позволяет сравнивать отклонения при контроле качества лабораторных тестов.