Модель Марковица

Что такое модель Марковица?

Модель Марковица — это метод максимизации доходности в рамках расчетного риска. Ее также называют портфельной теорией Марковица или современной портфельной теорией. Эта модель облегчает практическое применение; многие новые инвесторы используют этот метод на рынках капитала.

Модель выбора Марковица в основном фокусируется на диверсификации портфеля. Он разделяет акции на активы с высоким и низким риском. Модель Гарри Марковица была представлена ​​в 1952 году в финансовом журнале. Гарри Марковиц получил Нобелевскую премию за свой вклад в 1990 году.

Оглавление

• Что такое модель Марковица?
  • Объяснение модели управления портфелем Марковица
  • Предположения
  • Диаграмма
  • Формула
  • Пример расчета
  • Преимущества и недостатки
  • Часто задаваемые вопросы (FAQ)
  • Рекомендуемые статьи

Ключевые выводы

• Модель Марковица — это инвестиционная стратегия. Инвесторы-любители используют его, чтобы максимизировать валовую прибыль в пределах диапазона устойчивого риска.
• Модель Гарри Марковица была впервые опубликована в журнале «Финансы» в 1952 году. В 1990 году Гарри Марковиц получил Нобелевскую премию за свою работу по современной портфельной теории.
• Ограничения модели Марковица включают чрезмерную зависимость от исторических данных, нерелевантные предположения и использование средней дисперсии вместо потенциальных рисков.
• Предположения Марковица становятся неуместными; это особенно характерно для волатильных рынков.

Объяснение модели портфеля Марковица

Модель Марковица — это метод инвестирования. Он используется для создания портфеля, который будет приносить максимальную прибыль. В 1952 году Гарри Марковиц опубликовал свою модель в Journal of Finance. Марковиц — американский экономист. Он считается создателем современной портфельной теории. Эта теория также известна как модель средней дисперсии Марковица.

Модель портфеля Марковица предполагает, что риски можно минимизировать за счет диверсификации. В то же время модель обеспечивает максимизацию общей доходности портфеля. Инвесторам предлагается два типа акций: акции с низким риском и низкой доходностью и акции с высоким риском и высокой доходностью. Риски также делятся на два вида: систематический риск и несистематический риск. Модель Гарри Марковица использует математические расчеты для снижения рисков; он создает идеальное портфолио.

Тем не менее, реальные инвестиции не могут устранить определенный уровень риска. Таким образом, инвесторы должны обладать некоторой склонностью к риску. Новые инвесторы особенно выигрывают от этой теории — модель портфеля Марковица популяризировала диверсификацию. Не говоря уже о важности понимания и предотвращения систематических портфельных рисков.

С другой стороны, ограничения модели Марковица связаны с ее чрезмерным доверием к предположениям. Эти недостатки могут сделать выводы нерелевантными для преобладающих рыночных условий.

Предположения

Предположения Марковица следующие:

• Модель предполагает, что инвесторы рациональны и всегда будут вести себя определенным образом.
• Модель предполагает, что существует только два разных типа активов — низкодоходные и высокодоходные.
• Гарри Марковиц утверждает, что рынки всегда будут работать в определенном направлении и всегда будут эффективными. Но это не всегда так.
• Диверсификация важна. Но теория предполагает, что диверсификация — единственный способ минимизировать инвестиционные риски.
• Модель портфеля Марковица предполагает, что каждый инвестор имеет неограниченный доступ к информации об изменениях рынка. На самом деле инвесторам часто не хватает времени и опыта для сбора соответствующих данных.
• Марковиц предполагает, что все инвесторы не склонны к риску, но это не всегда верно.
• В модели упоминается порог терпимых убытков, но не все реальные инвесторы могут себе это позволить.

Диаграмма

Марковиц модель схема выглядит следующим образом.

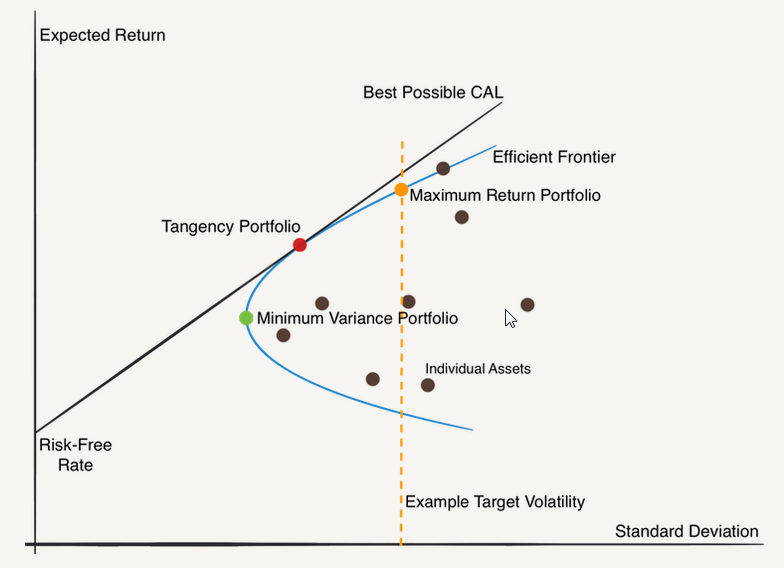(Источник)

Диаграмма Марковица изображает стандартное отклонение (риск) по оси x и ожидаемую доходность по оси y. На диаграмме показаны три портфеля:

1. Портфель с минимальной дисперсией
2. Касательный портфель
3. Портфель максимальной доходности

Граница эффективности представляет собой параболу, изображающую все три портфеля в направлении эффективности. Агентский портфель также является оптимальным — с самым высоким коэффициентом Шарпа.

Напротив, портфель с минимальной дисперсией — это зеленая точка на диаграмме. Он отмечает переход от выпуклого к вогнутому. Наконец, портфель максимальной доходности — это оранжевая точка — он имеет самую высокую волатильность.

В Марковице На диаграмме портфели на границе эффективности лучше портфелей под ней. Это связано с тем, что точка, в которой линейная линия рынка капитала (CML) касается оси Y, является безрисковым активом.

Формула модели Марковица

Марковиц формула выглядит следующим образом:

RP = IRF + (RM – IRF)σP/σM

Здесь,

• RP = ожидаемая доходность портфеля
• RM = доходность рыночного портфеля
• IRF = безрисковая процентная ставка
• σM = стандартное отклонение рынка
• σP = стандартное отклонение портфеля

Пример расчета

Давайте теперь посмотрим на Марковица Пример для лучшего понимания теории.

Предположим, что Чарли — инвестор с небольшим портфелем — всего две акции. Он инвестировал 900 000 долларов в акции А и 180 000 долларов в акции В — портфель в 1 080 000 долларов. Чарли ожидает доходность акций А в размере 4% и доходность акций Б в размере 9%.

Чтобы рассчитать ожидаемую доходность портфеля, мы делим текущую стоимость акции А на общую стоимость портфеля и умножаем ее на ожидаемую доходность:

• Ожидаемая доходность портфеля = 900 000 долл. США/1 080 000 x 4%.

Теперь мы повторяем шаг для второго актива:

• Ожидаемая доходность портфеля = $180 000/1080000 x 9%.

Итак, по акции А (наиболее инвестированной) Чарли получает ожидаемую доходность в размере 3%; для акции B (наименее инвестированной) Чарли получает ожидаемую доходность в размере 2%. Портфель может рассчитывать на доходность в размере 5%.

Чтобы увеличить ожидаемую доходность портфеля до 6,5%, Чарли необходимо переместить соответствующую сумму капитала в акции B (менее инвестированные).

Распределение капитала 50-50 приведет к следующим доходам:

Ожидаемая доходность портфеля 6,5%

• 50% х 4% = 2%

• Плюс 50% х 9% = 4,5%

• Ожидаемая доходность портфеля = 2% + 4,5% = 6,5%

Предположим, что Чарли делит портфель стоимостью 1 080 000 долларов на четыре равных актива. Бета первого актива равна 1, поэтому его систематический риск идентичен рыночному. Второй актив имеет бета 1,6, так как Чарли готов пойти на больший риск. Третий имеет бета-коэффициент 0,75 — меньше воздействия, чем рынок; четвертый имеет еще более низкую бета 0,5.

Умножение распределения 25% на соответствующие значения бета и сложение результатов дает Чарли общее значение бета портфеля 0,96. Поскольку он ниже 1, портфель считается систематическим риском.

Давайте рассмотрим другую гипотезу; Чарли перекладывает 10 % из третьего и четвертого активов с наименьшим бета-коэффициентом риска и 5 % из первого подразделения и инвестирует во второй актив (актив с наивысшим бета-коэффициентом). Здесь второй актив, который начинался с распределения 25%, станет 50% всего капитала портфеля, первый составляет 20%, а третье и четвертое подразделения составляют по 15% каждое.

• Бета первого дивизиона = 20% x 1 = 0,2

• Бета второго дивизиона = 50% x 1,6 = 0,8

• Бета третьего дивизиона = 15% x 0,75 = 0,11

• Бета четвертого деления = 15% x 0,5 = 0,08

• Новая бета будет равна 1,19, что близко к требуемому желаемому значению бета 1,2.

Преимущества и недостатки

Преимущества заключаются в следующем:

• Портфель становится устойчивым к систематическому риску
• Диверсификация помогает инвесторам понять различные сектора.
• Такие портфели подходят как для долгосрочного создания богатства, так и для получения краткосрочной прибыли.
• Разнообразие финансовых инструментов подходит для этой инвестиционной стратегии.

Недостатки следующие:

• Этот подход часто называют моделью средней дисперсии Марковица. Он более склонен к дисперсии и имеет тенденцию игнорировать потенциальные риски.
• Он не гарантирует хорошей доходности и основан только на исторических данных.
• Модель не учитывает сопутствующие расходы, такие как брокерские комиссии, налоги и другие сборы.
• Вся модель основана на нерелевантных допущениях фондового рынка. В действительности фондовые рынки столь же непредсказуемы, сколь и волатильны.

Часто задаваемые вопросы (FAQ)

1. Что такое модель Марковица оптимизации риска/доходности?

Модель Гарри Марковица гласит: акции в портфеле могут быть либо с низким риском и низкой доходностью, либо с высоким риском и высокой доходностью. Оптимизация обоих может помочь максимизировать общую доходность портфеля инвестора. Модель также определяет допустимый диапазон убытков в рамках портфеля, который инвестору, возможно, придется нести.

2. Каковы ограничения модели Марковица?

Ограничения модели Марковица следующие:
– Этот подход не основан на текущих данных; информация определяется через исторические данные.
– Модель основана на предположениях; иногда эти предположения становятся неуместными. Особенно это касается волатильных рынков.
– Это опора на дисперсию, когда в идеале следует сосредоточиться на рисках.

3. Почему важна модель Марковица?

Важными чертами теории Марковица являются следующие.
– Это помогает новым инвесторам-любителям в создании диверсифицированного портфеля.
– Теория помогает регулировать риски для минимизации потерь. В то же время инвестиции имеют хорошие шансы на получение прибыльной прибыли.
– Инвесторы могут использовать модель для выявления и замены неэффективных инвестиций.

Рекомендуемые статьи

Эта статья была руководством к тому, что такое модель Марковица. Мы объясняем его предположения, схему, формулу, расчеты, примеры, преимущества и недостатки. Подробнее об этом вы можете узнать из следующих статей —

• Блэк Литтерман Модель
• Ребалансировка портфеля
• Управление портфелем