Линия регрессии

Определение линии регрессии

Линия регрессии указывает на линейную связь между зависимыми переменными на оси y и независимыми переменными на оси x. Корреляция устанавливается путем анализа шаблона данных, сформированного переменными.

Линия регрессии строится ближе всего к точкам данных на графике регрессии. Этот статистический инструмент помогает анализировать поведение зависимой переменной y при изменении независимой переменной x путем подстановки различных значений x в уравнение регрессии.

Оглавление

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

Определение линии регрессии

Линия регрессии устанавливает линейную связь между двумя наборами переменных. Изменение одной переменной зависит от изменения другой (независимой переменной).
Линия регрессии методом наименьших квадратов (LSRL) строится ближе всего к точкам данных (x, y) на графике регрессии.
Регрессия широко используется в финансовых моделях, таких как CAPM, и инвестиционных показателях, таких как Beta, для определения осуществимости проекта. Он также используется для создания прогнозов инвестиций и финансовой отдачи.
Если Y является зависимой переменной, а X является независимой переменной, уравнение линии регрессии Y на X представляется следующим образом:
Y = a + bX + e.

Объяснение линии регрессии

Линия регрессии — это статистический инструмент, отображающий корреляцию между двумя переменными. В частности, он используется, когда изменение одной (зависимой переменной) зависит от изменения значения другой (независимой переменной).

Может быть два случая простой линейной регрессии:

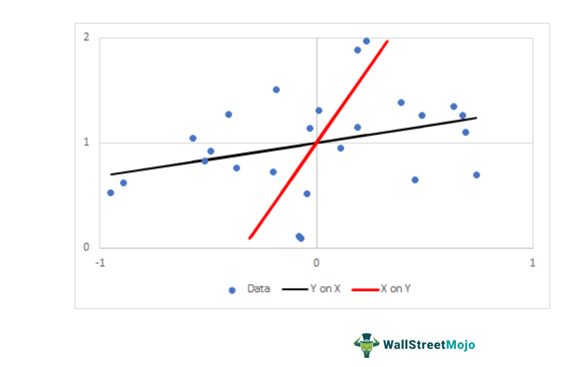
Уравнение Y на X, где значение Y изменяется с изменением значения X.
Уравнение представляет собой X на Y, где изменение переменной X зависит от отклонения переменной Y.

Регрессия широко применяется к различным сценариям реального мира — бизнесу, инвестициям, финансам и маркетингу. Например, в финансах регрессия в основном используется в BetaBetaBeta — это финансовая метрика, которая определяет, насколько чувствительна цена акции к изменениям рыночной цены (индекса). Он используется для анализа систематических рисков, связанных с конкретными инвестициями. В статистике бета — это наклон линии, который можно рассчитать путем регрессии доходности акций по отношению к рыночной доходности. Подробнее и Модель оценки капитальных активов (CAPMCAPMМодель оценки капитальных активов (CAPM) определяет ожидаемую доходность портфеля различных ценных бумаг с различной степени риска, а также учитывает волатильность конкретной ценной бумаги по отношению к рынку (подробнее) — для оценки доходности и составления бюджета.

Использование регрессииРегрессияРегрессионный анализ — это статистический подход к оценке взаимосвязи между 1 зависимой переменной и 1 или более независимыми переменными. Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читать далее, компания может определить соответствующую цену актива по отношению к стоимости капитала. На фондовом рынке он используется для определения влияния изменений цен на акции на цены базовых товаров.

В маркетинге регрессионный анализ можно использовать для определения того, как колебания цен приводят к увеличению или уменьшению продаж товаров. Он очень эффективен при составлении прогнозов продаж на будущий период — путем сопоставления рыночных условий, прогнозов погоды, экономических условий и прошлых продаж.

Формула

Формула для определения линии регрессии наименьших квадратов (LSRL) Y на X выглядит следующим образом:

Y=а + bX + е

Здесь,

Y — зависимая переменная.
a – Y-перехват.
b — наклон линии регрессии.
X — независимая переменная.
ɛ — невязка (ошибка).

Также,

b = (N∑XY-(∑X)(∑Y) / (N∑X2– (∑X)2) ;

И,

а = (∑Y – b ∑X) / N

Где N – общее количество наблюдений.

Пример

Давайте рассмотрим гипотетический пример, чтобы понять реальные приложения теории.

Финансовый менеджер ABC Motors хочет сопоставить колебания продаж и колебания цен на электрические велосипеды. Для этого он анализирует данные за последние пять лет.

Считаем, что ошибки нет. Цена и объем продаж за предыдущие пять лет следующие:

ГодЦена (в долларах)Объем продаж20172100150002018205016500201920002100020202200190002021205020000

По полученным данным определите линию регрессии Y по X,

Решение:

Определим линию регрессии Y на X:

Данный:

Y = объем продаж
Х = прибыль
Н = 5
ɛ =

ГодЦена (в долларах) (ИКС)Объем продаж (Y)х2XY20172100150004410000315000002018205016500420250033825000201920002100040000004200000020202200190004840000418000000202120504201200004201200000420120000042000000–104009150021655000190125000

Y = а + ЬХ + е

Сначала найдем значения b и a:

b = (N∑XY-(∑X)(∑Y) / (N∑X2– (∑X)2)

b = ((5×190125000) – (10400×91500)) / ((5×21655000) – 104002)
б = (950625000-951600000) / (08275000-108160000)
б = – 8,478

а = (∑Y – b ∑X) / N

а = 91500 – ( – 8,478 × 10400) / 5
а = 35935
Y = 35935 + (- 8,478 X) + 0
Y = 35935 – 8,478X

Данные представлены в виде линейного графика регрессии:

(Источник)

Визуализация собранных данных упрощает интерпретацию данных. Линию регрессии иногда называют линией наилучшего соответствия.

Важно отметить, что реальные данные не всегда могут быть выражены уравнением регрессии. Если большинство наблюдений следует шаблону, то выбросы могут быть устранены. Но иногда очевидной закономерности нет. При наличии случайных несоответствий в собранных данных метод регрессии не подходит.

Часто задаваемые вопросы (FAQ)

Что такое линия регрессии?

Линия регрессии изображает взаимосвязь между двумя переменными. Он применяется в сценариях, где изменение значения независимой переменной вызывает изменение значения зависимой переменной.

Как найти линию регрессии?

Формула линии регрессии для Y на X выглядит следующим образом:

Y = а + ЬХ + е
Здесь Y — зависимая переменная, a — точка пересечения Y, b — наклон линии регрессии, X — независимая переменная, а ε — невязка (ошибка).

Каков наклон линии регрессии?

Наклон линии регрессии обозначается буквой «b», которая показывает изменение зависимой переменной y, вызванное изменениями независимой переменной x. Формула для определения наклона линии регрессии для Y на X выглядит следующим образом:

b = (N∑XY-(∑X)(∑Y) / (N∑X2– (∑X)2)

Линия регрессии

Определение линии регрессии