Квартильная формула

Формула для расчета квартиля в статистике

Формула квартилей — это статистический инструмент для расчета дисперсии заданных данных путем деления их на четыре определенных интервала, сравнения результатов со всем набором наблюдений и комментирования различий в наборах данных.

Он часто используется в статистике для измерения дисперсий, которые описывают разделение всех данных наблюдений на четыре определенных интервала на основе значений данных и того, где они находятся по сравнению со всем набором данных наблюдений.

Он делится на 3 точки: нижний квартиль, обозначаемый Q1, который находится между наименьшим значением и медианой данного набора данных. Медиана, обозначаемая Q2, является медианой, а верхний квартиль, обозначаемый Q3, представляет собой среднюю точку между медианой. Медианная формула в статистике используется для определения среднего числа в наборе данных, расположенном в порядке возрастания. Медиана = {(n+1)/2}поток больше и наибольшее число в заданном наборе данных распределения.

Формула квартиля в статистике представлена ​​следующим образом:

Формула квартилей для Q1= ¼(n+1)-го члена Формула квартилей для Q3= ¾(n+1)-го члена Формула квартилей для Q2= Q3–Q1 (эквивалентно медиане)

Объяснение

Квартили будут делить измерения данного набора данных или выборки на четыре одинаковые или равные части. Например, 25% измерений данного набора данных (представленных Q1) не превышают нижний квартиль. 50% измерений не превышают медианы, т. е. Q2; наконец, 75% будет меньше, чем верхний квартиль, который обозначает Q3. Следовательно, 50% измерений данного набора данных находятся между Q1, нижним квартилем, и Q2, верхним квартилем.

Примеры

Давайте рассмотрим несколько простых и сложных примеров квартилей в excelQuartile. В функциях ExcelQuartile используются для поиска различных квартилей в наборе данных и они являются частью статистических функций Excel. Есть три квартили; первый квартиль (Q1) — это среднее число между наименьшим значением и медианным значением набора данных. Второй квартиль (Q2) является медианой данных. Третий квартиль (Q3) — это среднее значение между медианой набора данных и максимальным значением. Чтобы лучше понять его, прочитайте больше.
.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%}

Вы можете скачать этот шаблон формулы квартиля Excel здесь – Формула квартиля Excel Шаблон

Пример №1

Рассмотрим набор данных из следующих чисел: 10, 2, 4, 7, 8, 5, 11, 3, 12. Вам необходимо вычислить все 3 квартили.

Решение:

Используйте следующие данные для расчета квартиля.

Расчет медианы или Q2 можно выполнить следующим образом:

Медиана или Q2 = Сумма (2+3+4+5+7+8+10+11+12)/9

Медиана или Q2 будет –

Медиана или Q2 “=” 7

Поскольку количество наблюдений нечетное, то есть 9, медиана будет лежать на 5-й позиции, то есть 7, и то же самое будет Q2 для этого примера.

Расчет Q1 можно выполнить следующим образом:

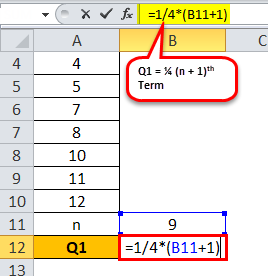
Q1= ¼ (9 + 1)

= ¼ (10)

Q1 будет –

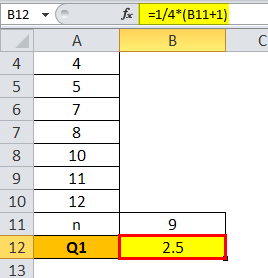
Q1 “=” 2,5

Это означает, что Q1 является средним значением 2-й и 3-й позиций наблюдений, которые здесь равны 3 и 4, а среднее значение того же равно (3 + 4)/2 = 3,5.

Расчет Q3 можно выполнить следующим образом:

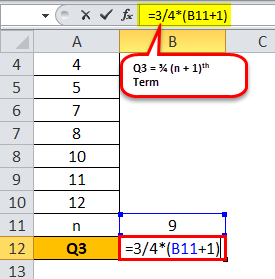
Q3 = ¾ (9 + 1)

= ¾ (10)

Q3 будет –

Q3 “=” 7.5 Срок

Это означает, что Q3 является средним значением 8-й и 9-й позиций наблюдений, которые здесь равны 10 и 11. То же самое среднее равно (10+11)/2 = 10,5.

Пример #2

Simple Ltd. — производитель одежды, работающий по схеме, чтобы порадовать своих сотрудников за их усилия. Руководство обсуждает запуск новой инициативы, в которой говорится, что они хотят разделить своих сотрудников следующим образом:

• Верхние 25%, лежащие выше Q3 – 25 долларов за ткань
• Больше, чем средний, но меньше, чем Q3 — 20 долларов за ткань.
• Больше, чем Q1, но меньше, чем Q2 — 18 долларов за ткань.
• Руководство собрало среднесуточные данные о производительности за последние 10 дней в расчете на одного (среднего) работника.
• 55, 69, 88, 50, 77, 45, 40, 90, 75, 56.
• Используйте формулу квартилей для построения структуры вознаграждения.
• Какое вознаграждение получит сотрудник, если он произведет 76 готовых вещей?

Решение:

Используйте следующие данные для расчета квартиля.

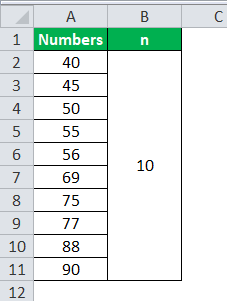Количество наблюдений здесь равно 10, и нашим первым шагом будет преобразование приведенных выше необработанных данных в порядке возрастания.
40, 45, 50, 55, 56, 69, 75, 77, 88, 90
Расчет квартиля Q1 может быть следующим:

Q1 = ¼ (n+1)-й член

= ¼ (10+1)

= ¼ (11)

Q1 будет –

Q1 “=” 2.75 Срок

Здесь необходимо взять среднее значение, состоящее из 2-го и 3-го членов, которые равны 45 и 50. Формула рассчитывается путем сложения всех значений заданного набора, обозначаемого суммированием X, и деления его на количество значений, заданных в наборе, обозначаемом N. Подробнее о том же: (45 + 50) / 2 = 47,50

Q1 составляет 47,50, что составляет 25% минимума.

Расчет квартиля Q3 можно выполнить следующим образом:

Q3 = ¾ (n+1)-й член

= ¾ (11)

Q3 будет –

Q3 “=” 8.25 Срок

Здесь необходимо взять среднее значение 8-го и 9-го членов, то есть 88 и 90. Среднее значение равно (88 + 90) / 2 = 89,00.

Q3 — 89, что составляет 25% лучших.

Расчет медианы или Q2 может быть следующим:

Среднее значение (Q2) = 8,25 – 2,75.

Медиана или Q2 будет –

Медиана или Q2“=” 5.5 Срок

Здесь необходимо взять среднее значение, которое составляет 5 и 6 56 и 69. Среднее значение равно (56 + 69) / 2 = 62,5.

Q2 или медиана составляет 62,5.

Что составляет 50% населения.

Диапазон вознаграждения будет следующим:

47.50 — 62.50 — 18 долларов за ткань.

> 62,50 — 89 получат 20 долларов за ткань

> 89,00 получите 25 долларов за ткань

Если работник производит 76, он будет лежать выше Q1. Следовательно, будет иметь право на бонус в размере 20 долларов.

Пример №3

Преподавание частных коуч-классов предполагает вознаграждение студентов из верхних 25% квартили советами межквартильным студентам, находящимся в этом диапазоне, и повторным сдачей занятий для студентов, находящихся ниже Q1. Используйте формулу квартиля, чтобы определить, с какими последствиями он столкнется, если он наберет в среднем 63 балла. .

Решение :

Используйте следующие данные для расчета квартиля.

Данные для 25 студентов.

Количество наблюдений здесь равно 25, и нашим первым шагом будет преобразование приведенных выше необработанных данных в порядке возрастания.
Расчет квартиля Q1 может быть следующим:

Q1 = ¼ (n+1)-й член

= ¼ (25+1)

= ¼ (26)

Q1 будет –

Q1 “=” 6.5 Срок

Q1 составляет 56,00, что составляет нижние 25%

Расчет квартиля Q3 можно выполнить следующим образом:

Q3 = ¾ (n+1)-й член

= ¾ (26)

Q3 будет –

Q3 “=” 19.50 Срок

Здесь необходимо взять среднее значение 19-го и 20-го членов, то есть 77 и 77. Среднее значение равно (77+77)/2 = 77,00.

Q3 составляет 77, что составляет 25% лучших.

Медиана или Q2 будет –

Медиана или Q2=19,50 – 6,5

Медиана или Q2 будет –

Медиана или Q2 “=” 13 Срок

Q2 или медиана составляет 68,00.

Что составляет 50% населения.

ргнев будет:

56.00 – 68.00

>68.00 – 77.00

77.00

Актуальность и использование формулы квартилей

Квартили позволяют быстро разделить заданный набор данных или выборку на четыре основные группы, упрощая пользователю оценку того, к какой из четырех групп относится точка данных. В то время как медиана, которая измеряет центральную точку набора данных, является надежной оценкой местоположения. Он не говорит, насколько данные наблюдений лежат на той или иной стороне или рассеяны или разбросаны. Квартиль измеряет разброс или дисперсию. В статистике дисперсия (или разброс) — это средство описания степени распределения данных вокруг центрального значения или точки. Это помогает понять распределение данных. Подробнее о значениях выше и ниже среднего арифметического Среднее арифметическое Среднее арифметическое обозначает среднее значение всех наблюдений ряда данных. Это совокупность всех значений в наборе данных, деленная на общее количество наблюдений или среднее значение, разделяющее распределение на четыре основные группы, описанные выше.

Рекомендуемые статьи

Эта статья была руководством по формуле квартилей. Здесь мы узнаем, как рассчитать квартили в статистике, используя ее формулу, практические примеры и загружаемый шаблон Excel. Вы можете узнать больше о моделировании в Excel из следующих статей:

• Оценщики баллов
• Квартильное отклонениеКвартильное отклонениеКвартильное отклонение основано на разнице между первым квартилем и третьим квартилем в частотном распределении, и эта разница также известна как межквартильный размах, разница, деленная на два, известна как квартильное отклонение или полумежквартильный размах.Подробнее
• Формула коэффициента вариацииФормула коэффициента вариацииКоэффициент вариации – это систематизированная мера дисперсии вероятностного или частотного распределения. Он определяется как отношение стандартного отклонения к среднему. читать далее
• Вычислить коэффициент корреляцииВычислить коэффициент корреляцииКоэффициент корреляции, иногда называемый коэффициентом взаимной корреляции, представляет собой статистическую меру, используемую для оценки силы взаимосвязи между двумя переменными. Его значения варьируются от -1,0 (отрицательная корреляция) до +1,0 (положительная корреляция). читать далее