Формула регрессионного анализа

Формула регрессионного анализа

Регрессионный анализ — это взаимосвязь между зависимыми и независимыми переменными, поскольку он показывает, как будут меняться зависимые переменные, когда одна или несколько независимых переменных изменяются из-за факторов. Следовательно, формула для расчета: Y = a + bX + E, где Y — зависимая переменная, X — независимая переменная, a — точка пересечения, b — наклон, а E — невязка.

Регрессия — это статистический инструмент для прогнозирования зависимой переменной с помощью одной или нескольких независимых переменных. При проведении регрессионного анализа основная цель исследователя – выяснить взаимосвязь между зависимыми и независимыми переменными. Выбирается одна или несколько независимых переменных, которые могут помочь предсказать зависимую переменную для предсказания зависимой переменной. Кроме того, это помогает проверить, достаточно ли хороши переменные-предикторы, чтобы помочь предсказать зависимую переменную.

Формула регрессионного анализа пытается найти линию наилучшего соответствия для зависимой переменной с помощью независимых переменных. Уравнение регрессионного анализа такое же, как и уравнение для линии:

у = МХ + б

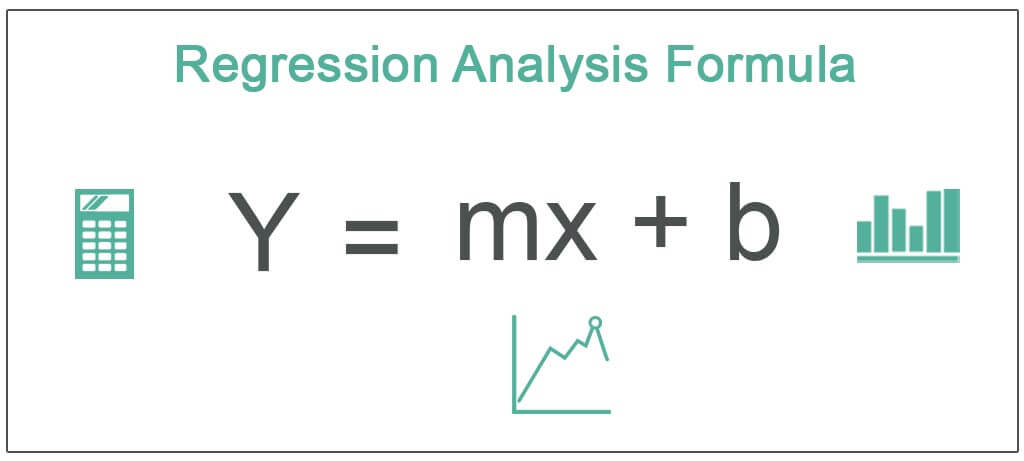
Где,

• Y = зависимая переменная уравнения регрессии
• M = наклон уравнения регрессии
• x=зависимая переменная уравнения регрессии
• B = постоянная уравнения

Оглавление

• Формула регрессионного анализа
  • Объяснение
  • Примеры
  • Актуальность и использование
  • Рекомендуемые статьи

Объяснение

При проведении регрессии основная цель исследователя – выяснить взаимосвязь между зависимыми и независимыми переменными. Затем одна или несколько независимых переменных помогают предсказать зависимую переменную. Регрессионный анализ помогает в процессе проверки того, достаточно ли хороши переменные-предикторы, чтобы помочь в прогнозировании зависимой переменной.

Примеры

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel формулы регрессионного анализа здесь – Формула регрессионного анализа Шаблон Excel

Пример №1

Давайте попробуем понять концепцию регрессионного анализа на примере. Во-первых, попробуем выяснить связь между расстоянием, пройденным водителем грузовика, и возрастом водителя грузовика. Затем кто-то составляет уравнение регрессии, чтобы проверить, подтверждается ли то, что он думает об отношениях между двумя переменными, уравнением регрессии.

Ниже приведены данные для расчета

Формула регрессионного анализа для приведенного выше примера будет иметь вид

• у = МХ + б
• у= 575,754*-3,121+0
• у = -1797

В этом конкретном примере мы увидим, какая переменная является зависимой, а какая независимой. Зависимой переменной в этом уравнении регрессии является расстояние, пройденное водителем грузовика, а независимой переменной — возраст водителя грузовика. Регрессия для этого набора зависимых и независимых переменных доказывает, что независимая переменная является хорошим предиктором зависимой переменной с достаточно высоким коэффициентом детерминацииКоэффициент детерминацииКоэффициент детерминации, также известный как R в квадрате, определяет степень дисперсии зависимой переменной что можно объяснить независимой переменной. Следовательно, чем выше коэффициент, тем лучше уравнение регрессии, так как это означает, что независимая переменная выбрана с умом. Подробнее. Кроме того, анализ помогает проверить правильность выбора факторов в виде независимой переменной. На снимке ниже показаны выходные данные регрессии для переменных. Набор данных и переменные представлены в прикрепленном листе Excel.

Пример #2

Давайте попробуем понять регрессионный анализ с помощью другого примера. Попробуем выяснить связь между ростом учеников класса и средним баллом этих учеников. Затем кто-то составляет уравнение регрессии, чтобы проверить, подтверждается ли то, что он думает об отношениях между двумя переменными, уравнением регрессии.

В данном примере ниже приведены данные для расчета в excel

Для расчета регрессионного анализа перейдите на вкладку «Данные» в Excel и выберите опцию «Анализ данных».

Регрессия для приведенного выше примера будет

• у = МХ + б
• у = 2,65 * 0,0034 + 0
• у = 0,009198

В этом конкретном примере мы увидим, какая переменная является зависимой, а какая независимой. Зависимой переменной в этом уравнении регрессии является средний балл учащегося, а независимой переменной — рост учащегося. Регрессионный анализ для этого набора зависимых и независимых переменных доказывает, что независимая переменная не является хорошим предиктором зависимой переменной, поскольку значение коэффициента детерминации незначительно. В этом случае нам нужно найти другую предикторную переменную, чтобы предсказать зависимую переменную для регрессионного анализа. На снимке ниже показаны выходные данные регрессии для переменных. Набор данных и переменные представлены в прикрепленном листе Excel.

Актуальность и использование

Регрессия — очень полезный статистический метод. Можно проверить любое бизнес-решение, чтобы подтвердить гипотезу о том, что конкретное действие повысит прибыльность подразделения на основе регрессии. Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читайте больше между зависимыми и независимыми переменными. Поэтому уравнение регрессионного анализа играет очень важную роль в финансах. Кроме того, многие прогнозы выполняются с использованием регрессии. Например, можно заранее предсказать продажи определенного сегмента с помощью макроэкономических показателей, которые имеют очень хорошую корреляцию с этим сегментом. Как линейная, так и множественная регрессия. Множественная регрессия. Формула множественной регрессии используется при анализе связи между зависимыми и многочисленными независимыми переменными. Формула = y = mx1 + mx2+ mx3+ хлеб больше полезна для практиков, чтобы делать прогнозы зависимых переменных и проверять независимые переменные как предикторы зависимых переменных.

Рекомендуемые статьи

Эта статья была руководством по формуле регрессионного анализа. Здесь мы обсуждаем выполнение регрессионных вычислений с использованием анализа данных, примеров и загружаемого шаблона Excel. Вы можете узнать больше о статистическом моделировании из следующих статей:

• Определение коэффициента ДжиниОпределение коэффициента ДжиниКоэффициент Джини или индекс Джини представляет собой статистическую дисперсию, отражающую дисперсию доходов среди населения страны, т.е. он представляет собой имущественное неравенство граждан конкретной страны. читать далее
• Регрессионный анализ ExcelRegression Анализ ExcelRegression выполняется для определения взаимосвязей между двумя или более переменными в наборе данных в статистической регрессии, выполняемой с помощью некоторых сложных формул. Тем не менее, Excel предоставил нам инструменты для регрессионного анализа. Итак, исследование взяло парк Excel, нажало на анализ данных, а затем на регрессионный анализ в Excel.Подробнее
• Формула R в квадратеФормула R в квадратеФормула R в квадрате описывает возможность возникновения события в рамках ожидаемого результата. Это «r = n (∑xy) – ∑x ∑y / √ [n* (∑x2 – (∑x)2)] * [n* (∑y2 – (∑y)2)] “, где r — коэффициент корреляции, n — число в данном наборе данных, x — первая переменная в контексте, а y — вторая переменная. читать далее
• ПримерыПримерыЛинейная регрессия представляет отношение между одной зависимой переменной и одной или несколькими независимыми переменными. Примерами линейной регрессии являются взаимосвязь между ежемесячными продажами и расходами, уровнем IQ и результатами тестов, ежемесячными температурами и продажами кондиционеров, населением и мобильными продажами. Подробнее о линейной регрессии