Формула регрессии

Формула для расчета регрессии

Формула регрессии оценивает взаимосвязь между зависимой и независимой переменными и выясняет, как она влияет на зависимую переменную при изменении независимой переменной. Он представлен уравнением Y равно aX плюс b, где Y — зависимая переменная, a — наклон уравнения регрессии, x — независимая переменная, а b — константа.

Регрессионный анализ широко использовал статистические методы для оценки отношений между одной или несколькими независимыми переменными и зависимыми переменными. РегрессияРегрессияРегрессионный анализ — это статистический подход к оценке взаимосвязи между 1 зависимой переменной и 1 или более независимыми переменными. Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. Читать дальше — мощный инструмент, поскольку он оценивает силу взаимосвязи между двумя или более переменными. Затем можно было бы использовать его для моделирования будущих отношений между этими переменными.

Y=a + bX + ∈

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

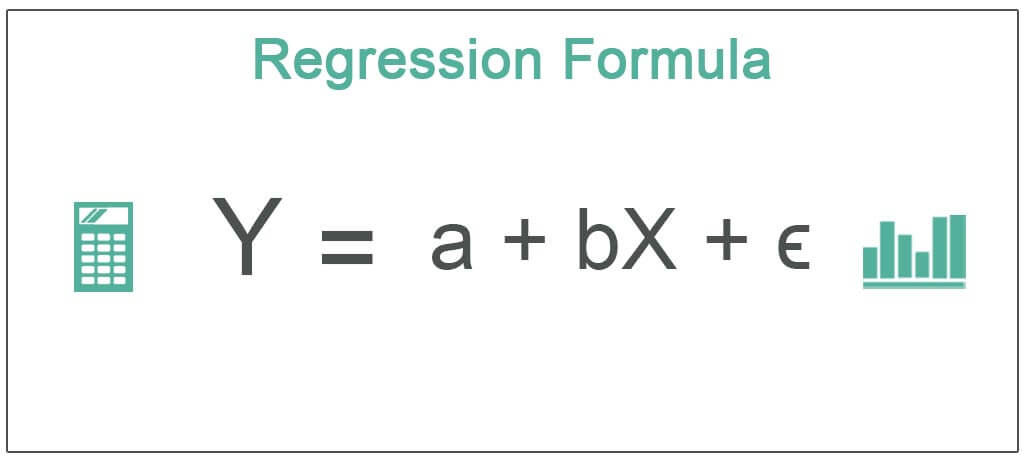
Где:

Y – зависимая переменная
X – независимая (объясняющая) переменная
а – перехват
б – уклон
∈ – и является невязкой (ошибкой)

Формула для пересечения «а» и наклона «b» может быть рассчитана, как показано ниже.

а= (Σy)(Σx2) – (Σx)(Σxy)/n(Σx2) – (Σx)2
б = п (Σxy) – (Σx)(Σy) /n(Σx2) – (Σx)2

Оглавление

Формула для расчета регрессии

Объяснение

Регрессионный анализ, как упоминалось ранее, в основном используется для поиска уравнений, которые будут соответствовать данным. Линейный анализ — это один из видов регрессионного анализа. Например, уравнение для линии y = a + bX. Y является зависимой переменной в формуле, которая пытается предсказать, какой будет будущая стоимость. Будущая стоимость Формула будущей стоимости (FV) — это финансовая терминология, используемая для расчета стоимости денежного потока на футуристическую дату по сравнению с исходным чеком. Цель уравнения FV состоит в том, чтобы определить будущую стоимость предполагаемых инвестиций и определить, приносят ли доходы достаточную прибыль, чтобы учесть временную стоимость денег. Подробнее, если X, независимая переменная, изменяется на определенное значение. «а» в формуле — точка пересечения. Это означает, что значение остается постоянным независимо от изменений независимой переменной. Термин «b» в формуле представляет собой наклон, который означает, насколько зависимая переменная зависит от независимой переменной.

Примеры

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон формулы регрессии Excel здесь – Шаблон Excel с формулой регрессии

Пример №1

Рассмотрим следующие две переменные x и y, необходимые для расчета регрессии.

Решение:

Используя приведенную выше формулу, мы можем рассчитать линейную регрессию в ExcelЛинейная регрессия В ExcelЛинейная регрессия — это статистический инструмент Excel, который используется в качестве модели прогнозирующего анализа для изучения взаимосвязи между двумя наборами данных. Используя этот анализ, мы можем оценить взаимосвязь между зависимыми и независимыми переменными следующим образом.

У нас есть все значения в приведенной выше таблице с n = 5.

Теперь сначала вычислите точку пересечения и наклон регрессии.

Расчет Intercept выглядит следующим образом:

а = (628,33 * 88 017,46) – (519,89 * 106 206,14) / 5 * 88 017,46 – (519,89)2

а = 0,52

Расчет уклона выглядит следующим образом:

b = (5 * 106 206,14) – (519,89 * 628,33) / (5 * 88 017,46) – (519,89)2

б = 1,20

Давайте теперь введем значения в формулу регрессии, чтобы получить регрессию.

Отсюда линия регрессии У = 0,52 + 1,20 * Х

Пример #2

Государственный банк Индии недавно ввел новую политику, связывающую процентные ставки по сберегательным счетам со ставками репо. Поэтому аудитор Государственного банка Индии хочет провести независимый анализ решений, принятых банком в отношении изменения процентной ставки, и того, были ли они изменены всякий раз, когда происходили изменения в ставке репо. Таким образом, ниже приводится сводная информация о ставке репо и процентной ставке по сберегательному счету Банка, которая преобладала в эти месяцы.

Аудитор Государственного банка Индии обратился к вам с просьбой провести анализ и представить презентацию на следующем собрании. Используйте формулу регрессии и определите, изменилась ли ставка банка, как и когда она изменила ставку репо.

Решение:

Используя формулу, рассмотренную выше, мы можем рассчитать линейную регрессию в Excel. Обращение с RepoRepoСоглашение об обратном выкупе или репо представляет собой краткосрочное заимствование для физических лиц, которые имеют дело с государственными ценными бумагами. Такое соглашение может заключаться между несколькими сторонами в трех типах: специализированная поставка, репо с хранением и репо с третьей стороной. Читать далее ставка как независимая переменная, т. е. X, и учет ставки банка как зависимой переменной как Y.

У нас есть все значения в приведенной выше таблице с n = 6.

Теперь сначала вычислите точку пересечения и наклон регрессии.

Расчет Intercept выглядит следующим образом:

а = (24,17 * 237,69) — (37,75 * 152,06) / 6 * 237,69 — (37,75)2

а = 4,28

Расчет уклона выглядит следующим образом:

б = (6 * 152,06) – (37,75 * 24,17) / 6 * 237,69 – (37,75)2

б= -0,04

Давайте теперь введем значения формул, чтобы получить фигуру.

Следовательно, линия регрессии Y = 4,28 – 0,04 * X.Анализ: Государственный банк Индии действительно следует правилу связывания своей ставки сбережений со ставкой репо, поскольку некоторое значение наклона указывает на связь между ставкой репо и ставкой сберегательного счета банка.

Пример №3

Лаборатория ABC исследует рост и вес и хотела знать, есть ли какая-либо связь, например, по мере увеличения роста будет увеличиваться и вес. Итак, они собрали выборку из 1000 человек для каждой категории и нашли средний рост в этой группе.

Ниже приведены детали, которые они собрали.

Вам необходимо выполнить расчет регрессии и сделать вывод, что такие отношения существуют.

Решение:

Используя формулу, рассмотренную выше, мы можем рассчитать линейную регрессию в Excel. Рассматривая рост как независимую переменную, т. е. X, а вес как зависимую переменную как Y.

У нас есть все значения в приведенной выше таблице с n = 6

Теперь сначала вычислите точку пересечения и наклон регрессии.

Расчет Intercept выглядит следующим образом:

а = (350 * 120 834) — (850 * 49 553) / 6 * 120 834 — (850)2

а = 68,63

Расчет уклона выглядит следующим образом:

б = (6 * 49 553) – (850 * 350) / 6 * 120 834 – (850)2

б = -0,07

Давайте теперь введем значения в формулу, чтобы получить цифру.

Отсюда линия регрессии Y = 68,63 – 0,07 * X

Анализ: Существует значительная, меньшая зависимость между ростом и весом, так как уклон очень низкий.

Актуальность и использование формулы регрессии

Когда коэффициент корреляцииКоэффициент корреляцииКоэффициент корреляции, иногда называемый коэффициентом взаимной корреляции, является статистической мерой, используемой для оценки силы взаимосвязи между двумя переменными. Его значения варьируются от -1,0 (отрицательная корреляция) до +1,0 (положительная корреляция). Читать дальше показывает, что данные могут предсказывать будущие результаты. Наряду с этим, точечная диаграмма одного и того же набора данных выглядит как линейная или прямая линия. Можно использовать простую линейную регрессию, используя наилучшее соответствие, чтобы найти прогностическое значение или прогностическую функцию. Регрессионный анализ имеет множество применений в финансах, поскольку он используется в CAPM, модели ценообразования капитальных активовМодель ценообразования капитальных активовМодель ценообразования капитальных активов (CAPM) определяет ожидаемый доход от портфеля различных ценных бумаг с различной степенью риска. Он также учитывает волатильность конкретной ценной бумаги по отношению к рынку. Читать далее метод в финансах. Его можно использовать для прогнозирования доходов и расходов фирмы.