Формула распределения выборки

Что такое формула выборочного распределения?

Распределение выборки определяется как вероятностное распределение конкретных статистических данных. Его формула помогает вычислить средние значения выборки, диапазон, стандартное отклонение и дисперсию.

Для размера выборки более 30 формула распределения выборки приведена ниже:

µ͞x =µ и σ͞x =σ / √n

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

Здесь,

Среднее значение выборки и совокупности, представленное µ͞x и µ.
Стандартное отклонение выборки и генеральной совокупности представлено как σ͞x и σ.
Размер выборки более 30 представлен как n.

Оглавление

Что такое формула выборочного распределения?

Объяснение

Можно рассчитать формулу для выборочного распределенияВыборочное распределениеВыборочное распределение представляет собой вероятностное распределение, использующее статистику, сначала выбирая конкретную совокупность, а затем используя случайные выборки, взятые из совокупности. Он нацелен на распространение частот, связанных с распространением различных результатов или результатов, которые могут иметь место для конкретной выбранной группы населения. Узнайте больше, используя следующие шаги:

Во-первых, найдите количество выборок, имеющих аналогичный размер n, из большей совокупности, имеющей значение N.
Затем разделите образцы в виде списка и определите среднее значение каждого образца.
Далее подготовьте Распределение частоты среднего значения выборки, как определено на шаге 2.
Затем определите распределение вероятностей определенных выборочных средних после определения частотного распределения на шаге 3.

Примеры формулы выборочного распределения (с шаблоном Excel)

Давайте рассмотрим несколько простых и сложных практических примеров уравнения распределения выборки, чтобы лучше понять его.

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel для формулы распределения выборки здесь – Формула распределения выборки Шаблон Excel

Пример №1

Берите пример с женского населения. Размер выборки составляет 100 человек со средним весом 65 кг и стандартным отклонением 20 кг. Помогите исследователю определить среднее значение и стандартное отклонение размера выборки из 100 женщин.

Решение

Используйте приведенные ниже данные для расчета выборочного распределения.

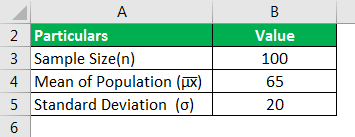
Среднее значение выборки эквивалентно среднему значению генеральной совокупности, поскольку размер выборки превышает 30.

Расчет стандартного отклонения размера выборки осуществляется следующим образом:

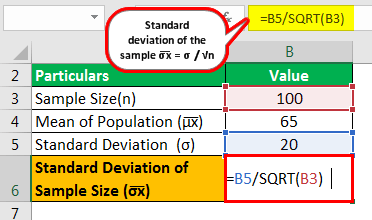
=20/√100

Стандартное отклонение размера выборки будет:

σx =2

Таким образом, стандартное отклонение выборки равно 2, а среднее значение выборки равно 65 кг.

Пример #2

Возьмем пример налогов, уплачиваемых транспортными средствами. В Калифорнии средний уплаченный налог составляет 12 225 долларов США при стандартном отклонении 5 000 долларов США. Они провели наблюдения за размером выборки из 400 грузовиков и прицепов вместе взятых. Помогите транспортному отделу определить среднее значение и стандартное отклонение выборки.

Решение

Используйте приведенные ниже данные для расчета выборочного распределения.

Расчет стандартного отклонения размера выборки осуществляется следующим образом:

= 5000 долларов США / √400

Стандартное отклонение размера выборкиФормула размера выборки отражает соответствующий диапазон генеральной совокупности, в которой проводится эксперимент или опрос. Он измеряется с использованием размера совокупности, критического значения нормального распределения при требуемом уровне достоверности, доли выборки и предела погрешности.

σ͞x = 250 долларов США

Следовательно, стандартное отклонение выборки, оцененное транспортным отделом, составляет 250 долларов, а среднее значение выборки — 12 225 долларов.

Пример №3

Давайте возьмем пример следующих данных, отображаемых ниже:

Пример Средней ЧастотыВероятности2020,672110,333010,33

Помогите исследователю определить среднее значение и стандартное отклонение выборки.

Определите среднее значение образца, как показано ниже: –

=20*0,67

Среднее будет –

=13,33

Общее среднее значение

=13,33+7+10
Общее среднее = 30,33

Определите дисперсию выборки, как показано ниже: –

=20^2*0,67
=266,66667

Дисперсия

Общая дисперсия

= 713,67

Расчет стандартного отклонения размера выборки осуществляется следующим образом:

σ͞x = √ 713,67 – 30,33

Стандартное отклонение будет –

σx = 26,141

Следовательно, стандартное отклонение выборки, оцененное исследователем, равно 26,141, а среднее значение выборки равно 30,33.

Актуальность и использование

Многие организации используют выборочное распределение для исследований. Это могут быть аналитики, исследователи и статистики. Когда население велико, такая методология помогает сформировать меньшую выборку, которую затем можно использовать для определения средних значений и стандартных отклонений. Средние средние значения могут быть нанесены на график для получения равномерного распределения. Равномерное распределение. Равномерное распределение — это тип распределения вероятностей, при котором каждый вероятный результат имеет одинаковую вероятность возникновения, и далее он подразделяется на непрерывное и дискретное распределение. Это представлено как прямая горизонтальная линия. подробнее о населении. Если исследователь увеличивает размер выборки, вероятность того, что график достигнет нормального распределения, увеличивается.

Это помогает значительно упростить выводы, используемые в статистике. Кроме того, это помогает вывести аналитическое соображение путем определения частоты распределения вероятностей. Распределение вероятностей. Распределение вероятностей можно определить как таблицу или уравнения, показывающие соответствующие вероятности различных возможных результатов определенного события или сценария. Простыми словами, его расчет показывает возможный исход события с относительной вероятностью наступления или ненаступления по мере необходимости. Подробнее о выборочных средствах. Наконец, выборочное распределение формирует основу для нескольких статистических концепций, которые исследователи могут использовать для обоснования своей гипотезы.