Формула множественной регрессии

Что такое формула множественной регрессии?

Формулы множественной регрессии анализируют взаимосвязь между зависимыми и несколькими независимыми переменными. Например, уравнение Y представляет собой формулу, которая равна плюс bX1 плюс cX2 плюс dX3 плюс E, где Y — зависимая переменная, а X1, X2 и X3 — независимые переменные. A — точка пересечения, b, c и d — наклоны, а E — остаточное значение.

у = тх1 + тх2+ тх3+ б

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

Где,

Y = зависимая переменная регрессии
M = наклон регрессии
X1=первая независимая переменная регрессии
x2=вторая независимая переменная регрессии
x3=третья независимая переменная регрессии
В= постоянная

Оглавление

Что такое формула множественной регрессии?

Объяснение формулы регрессионного анализа

Множественные регрессии — это метод прогнозирования зависимой переменной с помощью двух или более независимых переменных. При проведении этого анализа основная цель исследователя – выяснить взаимосвязь между зависимыми и независимыми переменными. Выбирается несколько независимых переменных, которые могут помочь предсказать зависимую переменную для предсказания зависимой переменной. Его можно использовать, когда линейная регрессия не может служить цели. Регрессионный анализ помогает в процессе проверки того, достаточно ли хороши переменные-предикторы, чтобы помочь в прогнозировании зависимой переменной.

Примеры

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel с формулой множественной регрессии здесь — Шаблон Excel с формулой множественной регрессии

Пример №1

Давайте попробуем понять концепцию множественного регрессионного анализа на примере. Но сначала попробуем выяснить зависимость между расстоянием, пройденным водителем UBER, и возрастом водителя, а также количеством лет стажа водителя.

Чтобы рассчитать множественную регрессию, перейдите на вкладку «Данные» в Excel и выберите параметр «Анализ данных». Для получения дополнительной информации о процедурах и расчетах см.: Пакет инструментов анализа в ExcelПакет анализа данных В Excel Пакет инструментов анализа данных Excel может использоваться пользователями для выполнения анализа данных и других важных вычислений. Его можно включить вручную в разделе надстроек на вкладке «Файлы», щелкнув «Управление надстройками», а затем проверив пакет инструментов для анализа. Читать далее статью.

Формула регрессииФормула регрессииФормула регрессии используется для оценки взаимосвязи между зависимой и независимой переменными и для определения того, как изменение независимой переменной влияет на зависимую переменную. Y = a + b X +читать дальше для приведенного выше примера будет

у = МХ + МХ + б
у= 604,17*-3,18+604,17*-4,06+0
у = -4377

В этом конкретном примере мы увидим, какая переменная является зависимой, а какая независимой. Зависимой переменной в этом регрессионном уравнении является расстояние, пройденное водителем UBER, а независимыми переменными — возраст водителя и его стаж вождения.

Пример #2

Давайте попробуем понять концепцию множественного регрессионного анализа с помощью другого примера. Попробуем найти связь между средним баллом класса студентов, количеством часов обучения и ростом студента.

Перейдите на вкладку «Данные» в Excel и выберите опцию «Анализ данных» для расчета.

Уравнение регрессии для приведенного выше примера будет

у = МХ + МХ + б

у = 1,08 * 0,03 + 1,08 * – 0,002 + 0

у = 0,0325

В этом конкретном примере мы увидим, какая переменная является зависимой, а какая независимой. Зависимой переменной в этой регрессии является средний балл, а независимыми переменными являются количество учебных часов и рост учащихся.

Пример №3

Давайте попробуем понять концепцию множественного регрессионного анализа с помощью другого примера. Теперь давайте выясним связь между заработной платой группы сотрудников в организации, количеством лет опыта и возрастом сотрудников.

Перейдите на вкладку «Данные» в Excel и выберите опцию «Анализ данных» для расчета.

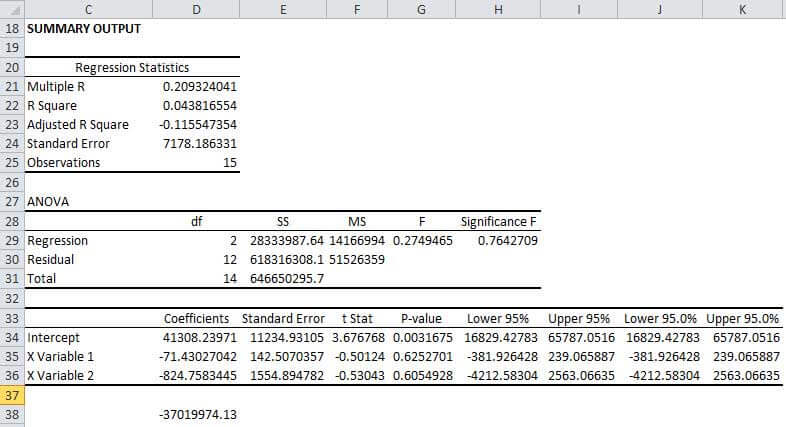
Уравнение регрессии для приведенного выше примера будет

у = МХ + МХ + б
у= 41308*.-71+41308*-824+0
у = -37019

В этом конкретном примере мы увидим, какая переменная является зависимой, а какая независимой. Зависимой переменной в этом уравнении регрессии является заработная плата, а независимыми переменными являются опыт и возраст сотрудников.

Актуальность и использование

Множественные регрессии — очень полезный статистический метод. Регрессия играет очень важную роль в мире финансов. Многие прогнозы выполняются с использованием регрессии. Регрессия. Регрессионный анализ — это статистический подход к оценке взаимосвязи между 1 зависимой переменной и 1 или более независимыми переменными. Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читать дальше анализ. Например, можно заранее предсказать продажи определенного сегмента с помощью макроэкономических показателей, которые имеют очень хорошую корреляцию с этим сегментом.