Байесовский вывод

Что такое байесовский вывод?

Байесовский вывод в математике — это метод определения статистического вывода для изменения или обновления вероятности события или гипотезы по мере поступления дополнительной информации. Следовательно, его также называют байесовским обновлением, и он играет важную роль в последовательном анализе и проверке гипотез.

Также называемая байесовской вероятностью, она основана на теореме Байеса. Байесовский вывод имеет множество применений из-за его важности в прогнозном анализе. Он широко используется и изучается в науке, математике, экономике, философии и т. д. Его потенциал в науке о данных выглядит особенно перспективным для машинного обучения.

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

Оглавление

Что такое байесовский вывод?

Байесовский вывод — это математический метод сопоставления новой информации (доказательств) с существующими данными. Таким образом, его важность может быть связана с постоянным требованием обновления данных и, следовательно, их полезности.
Байесовское обновление основано на теореме Байеса. Используя формулу, можно легко найти вероятность фактического события с учетом новых изменений.
Это всего лишь один из методов статистического вывода. Частотная вероятность – это еще один метод, который определяет вероятность на основе повторяющегося набора данных.

Объяснение байесовского вывода

Байесовский вывод в статистическом анализе можно понять, сначала изучив статистический вывод. Статистический вывод — это метод, используемый для определения характеристик распределения вероятностей и, таким образом, самой совокупности. Следовательно, байесовское обновление помогает обновлять характеристики населения по мере появления новых данных. Следовательно, его роль оправдана, так как для получения точных результатов необходима новая информация.

Теперь давайте систематически разберемся в технических аспектах байесовской модели вывода.

Теорема Байеса утверждает, что

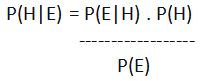
Здесь H — гипотеза или событие, вероятность которого была определена.

E — свидетельство или новые данные, которые могут повлиять на гипотезу.

P(H) — это априорная вероятность или вероятность гипотезы до того, как стали доступны новые данные.

P(E) — предельная вероятность и вероятность возникновения события.

P(E|H) — это вероятность того, что событие E произойдет при условии, что событие H уже произошло. Его также называют вероятностью.

P(H|E) является апостериорной вероятностью и определяет вероятность события H, когда событие E произошло. Следовательно, событие E является требуемым обновлением.

Таким образом, апостериорная вероятность увеличивается с вероятностью и априорной вероятностью, а уменьшается с предельной вероятностью.

Приложения

Байесовская сеть логического вывода имеет множество приложений. Например, он используется для статистического анализа данных, определения вероятности и прогнозного анализа. Вот несколько известных применений:

Растущее использование байесовской модели вывода в машинном обучении выглядит многообещающе. Например, он используется для разработки алгоритмов распознавания образов, фильтрации спама в электронной почте и т. д.
Биоинформатика и ее приложения в здравоохранении очень важны, особенно в общей модели риска рака и непрерывном индивидуальном индексе риска.
Присяжные используют байесовскую вероятность, чтобы определить вероятность конкретного дела по мере накопления новых доказательств.
Он также используется в исследованиях для определения вероятности события, когда становятся доступными новые наблюдения.
Наконец, байесовское обновление широко используется в финансах, торговле, маркетинге и экономике. Это зависит от человека, который использует эту технику, чтобы получить максимальную пользу.

Примеры

Давайте обсудим несколько примеров байесовского вывода в статистическом анализе.

Пример №1

В следующей таблице представлена информация о четырех группах людей, основанных на двух признаках — говорящих по-английски и читающих газету.

НаблюденияГоворит по-английски (Э)Не говорит по-английски (Э’)СУММАЧитает газету (N)203050Не читает газету (N’)251540SUM454590

Событие E относится к количеству людей, говорящих по-английски.

Событие E’ является логическим отрицанием E и относится к людям, которые не говорят по-английски.

Точно так же событие N относится к числу людей, прочитавших газету.

Событие N’ относится к количеству людей, которые не читают газету.

Таким образом, P(E) + P(E’) = 1

Поскольку общая вероятность всегда равна единице, люди могут говорить по-английски.

Точно так же P(N) + P(N’) = 1

Численность населения составляет 90 человек.

Итак, давайте вычислим вероятность N при заданном E, т. е. P(N|E).

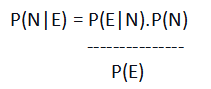
Р(Н) = 50/90

Р(Э) = 45/90

Р(Е|N) = 20/50

Таким образом, P(N|E) = [20/ 50 * 50/90]/ (45/ 90)

= 20/45

Но это можно сделать и непосредственно из таблицы (без использования формулы).

НаблюденияГоворит по-английски (Э)Не говорит по-английски (Э’)СУММАЧитает газету (N)303060Не читает газету (N’)251540SUM5545100

Теперь предположим, что число людей, говорящих по-английски и читающих газеты, увеличилось до 30.

Р(Н) = 60/100

Р(Э) = 55/100

Р(Е|N) = 30/60

Таким образом, P(N|E) = [30/ 60 * 60/100]/ (55/ 100)

= 30/55

Пример #2

Metanomic — компания-разработчик программного обеспечения, которая поддерживает разработчиков игр, моделируя игровую экономику, и играет значительную роль в создании Метавселенной. Недавно Metanomic приобрела Intoolab, биомедицинскую платформу на базе искусственного интеллекта. Intoolab первой разработала байесовский сетевой механизм искусственного интеллекта.

Приобретение поможет сторонам понимать огромный потенциал статистических методов, таких как байесовский вывод, и улучшить пользовательский опыт для игроков. Кроме того, технология Intoolab станет отличным дополнением к Metanomic, поскольку она объединяет игроков со всего мира в режиме реального времени.

Байесовский вывод против максимального правдоподобия против частотного анализа

Подобно байесовскому выводу, максимальное правдоподобие и частотность являются важными понятиями статистического вывода. Однако их подход и масштаб различны.

Как следует из названия, максимальная вероятность относится к состоянию, при котором вероятность того, что событие произойдет, является самой высокой. В статистике это достигается путем оценки наблюдаемого значения (параметров).
На основании определенных данных ученый определяет, что вероятность того или иного исхода составляет 65%. Но они хотят оценить, когда событие станет 100% вероятным. Поэтому они пытаются изменить данные, чтобы достичь максимальной вероятности, путем простых проб и ошибок.
Частотная вероятность, или частотность, определяет вероятность события, учитывая частоту конкретного наблюдения, т. е. сколько раз наблюдаются определенные данные. Частотизм и байесовский вывод часто считаются конкурирующими подходами.
Например, вероятность выпадения решки при подбрасывании монеты составляет 50%. Байесианец сказал бы, что это потому, что есть только две возможности — решка и решка. И вероятность появления любого из них одинакова. Тем не менее, частый игрок заявил бы, что вероятность составляет 50%, потому что, если монеты подбрасывались достаточное количество раз, решка выпадала в половине случаев.
Все эти концепции имеют важное применение в областях, где очень важны данные, таких как исследования, машинное обучение, бизнес и т. д.

Часто задаваемые вопросы (FAQ)

1. Является ли байесовский вывод машинным обучением?

Нет. Байесовский вывод нельзя соотносить с машинным обучением. Это может быть распространенной путаницей, поскольку она играет очень важную роль в искусственном интеллекте. Машинное обучение — лишь одно из многих применений байесовской вероятности.

2. Как работает байесовский вывод?

Байесовская вероятность учитывает новые свидетельства или данные для определения вероятности события, вероятность которого уже была оценена. Необходимо, чтобы по мере поступления новой информации менялись и системы, зависящие от данных. Это может быть чрезвычайно полезно в долгосрочной перспективе и позволяет избежать стагнации в системе, предоставляя пространство для роста.

3. Как вы делаете байесовский вывод?

Байесовская сеть вывода основана на теореме Байеса.
Р(Н|Е) = Р(Е|Н) . Р(Н)
——————
П(Э)
P(H) — вероятность события, рассчитанная ранее.
P(E) — вероятность того, что новая информация станет доступной недавно.
P(E|H) — вероятность новой информации при условии, что предыдущее событие уже произошло.
P(H|E) — это то, что нужно найти, и оно определяет вероятность более раннего события, приспосабливаясь к новой информации.

Байесовский вывод

Что такое байесовский вывод?