Равномерное распределение

Определение равномерного распределения

Равномерное распределение — это статистическое распределение, при котором каждый результат имеет равные шансы. Исследователи или бизнес-аналитики используют этот метод, чтобы проверить равную вероятность различных результатов, возникающих в течение определенного периода времени во время события. Это, в свою очередь, помогает им подготовиться ко всем ситуациям, имеющим равные шансы на возникновение.

Обозначая равновероятную вероятность, они изображаются горизонтальной линией, параллельной оси X, показывающей причину, событие или действие. Оно отличается от нормального распределения, что означает, что данные вокруг/близко к среднему значению встречаются часто.

Оглавление

• Определение равномерного распределения
  • Как работает равномерное распределение?
  • Типы
  • Приложение
  • Шаги к расчету равномерного распределения
  • Формула
  • Пример
  • Нормальное и равномерное распределение
  • Часто задаваемые вопросы (FAQ)
  • Рекомендуемые статьи

Ключевые выводы

• Равномерное распределение относится к типу распределения, отражающему однородность. Это означает, что каждый возможный исход причины, действия или события имеет равные шансы на возникновение.
• Дискретная и непрерывная — это две формы такого распределения, наблюдаемые в зависимости от типа ожидаемого результата.
• Подобно нормальному распределению, его равномерный аналог также симметричен по своей природе, т. е. обе стороны графика являются зеркальными отображениями друг друга.
• Когда пользователи наносят шансы на появление каждого результата на графике, получается линия, параллельная оси X.

Как работает равномерное распределение?

Вероятность равномерного распределения символизирует единообразие шансов различных результатов, происходящих из-за причины, действия или события. Когда пользователи отображают шансы появления каждого результата на графике, они получают линию, параллельную оси X, которая указывает шансы появления значений переменных на оси X.

Например, если кто-то хочет узнать вероятность того, что из колоды карт будет выбрана одна карта из червы, пики, бубны и трефы, каждая из них с одинаковой вероятностью будет выбрана всякий раз, когда игрок берет карту. Таким образом, каждая карта из колоды имеет 25% шанс выбора каждый раз, когда пользователь их достает. То же самое и с игральными костями, где каждое число имеет равные шансы выпасть всякий раз, когда игроки бросают и бросают его.

Типы

Равномерное распределение бывает двух видов – дискретным и непрерывным. Эта бифуркация зависит от типа исходов с возможностью возникновения.

А дискретное равномерное распределение это распределение вероятностей, при котором у исследователей есть предопределенное число равновероятных исходов. Например, бросая кости, игроки знают, что каким бы ни был результат, он будет варьироваться от 1 до 6. Здесь пользователи заранее определяют ожидаемые результаты и понимают, что вероятность наступления каждого результата составляет 1/6.

Другим является непрерывное распределение, которое не определяет ожидаемых событий. Также называемое прямоугольным распределением, учитывая прямоугольную форму, сформированную после нанесения значений на график, они обеспечивают равные шансы возникновения каждого результата, но не указывают количество вероятных эффектов / результатов, что означает бесконечное существование.

Приложение

Это симметричное распределение вероятностей. Таким образом, любое событие или эксперимент здесь может иметь произвольный исход для выбранных параметров или границ. Параметры a и b являются минимальной и максимальной границами. Существуют интервалы, либо открытый интервал, либо закрытый интервал, рассчитываемые как разница между максимальной и минимальной границами. Определение вероятностей в этой форме распределения легко оценить. Следовательно, он формирует основу для проверки гипотез и случаев выборки в дополнение к его использованию в финансах.

Шаги к расчету равномерного распределения

Однако исследователям или аналитикам необходимо выполнить следующие шаги, чтобы рассчитать ожидаемое значение равномерного распределения:

1. Оценивает максимальное и минимальное значения
2. Узнайте длину интервала, вычитая минимальное значение из максимального значения.
3. Следующим шагом является определение функции плотности вероятности. Здесь пользователь может разделить единицу на длину интервала.
4. Теперь найдите среднее значение значений.
5. Рассчитать дисперсия равномерного распределения.
6. Вычислите стандартное отклонение, найдя квадратный корень из дисперсии.

Формула

Значение ожидаемых результатов обычно равно среднему значению параметров a и b, которые являются параметрами минимального и максимального значения соответственно. Среднее будет:

Среднее значение равномерного распределения = (a+b)/2

Дисперсия равномерного распределения:

σ2 = b-a2/12

Функция плотности здесь:

F (х) = 1 / (ба)

Пример

Предположим, человек тратит на обед от 5 до 15 минут. Для ситуации давайте определим среднее значение и стандартное отклонение.

Вот данные, доступные для расчета.

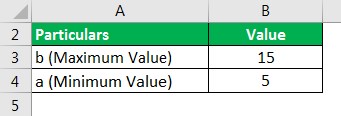
Среднее значение распределения

• = (15+5)/2

Среднее будет –

• Среднее = 10 минут

Далее, срасчет стандартного отклонения равномерного распределения будет –

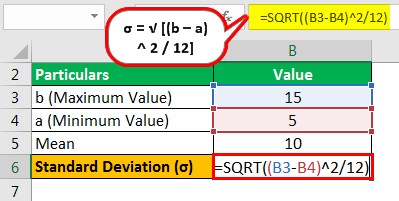
п = √ [(15 – 5)^ 2/ 12] = √ [(10)^ 2/ 12]

= √ [100 / 12]

= √ 8,33

Стандартное отклонение будет –

• σ = 2,887

Таким образом, распределение показывает среднее значение за 10 минут со стандартным отклонением 2,887 минуты.

Нормальное и равномерное распределение

Как равномерное, так и нормальное распределения симметричны, отображая линию по центру распределения при нанесении на график. Это означает, что одна сторона дистрибутива будет идеальным зеркальным отражением другой.

Хотя есть сходство, они существенно различаются по форме. В то время как нормальное распределение имеет форму колокола, его равномерный аналог имеет прямоугольную форму, что указывает на равновероятность возникновения различных результатов.

Часто задаваемые вопросы (FAQ)

Что такое равномерное распределение?

Это тип распределения вероятностей, при котором все исходы имеют равные шансы или имеют одинаковую вероятность произойти и могут быть разделены на непрерывное и дискретное распределение вероятностей. Обычно они изображаются прямыми горизонтальными линиями.

Когда использовать равномерное распределение?

Его можно использовать, когда исследователи, аналитики или пользователи знают, что любой объект/результат в выборочном пространстве будет иметь равные шансы на появление.

Как найти дисперсию равномерного распределения?

Пользователи могут найти дисперсию, вычитая минимальное значение из максимального значения, возведенного в степень двойки, а затем разделив полученное значение на двенадцать.

Рекомендуемые статьи

Это руководство о том, что такое равномерное распределение и его определение. Здесь мы объясним распределение вероятностей, его дисперсию, формулу и пример. Вы можете узнать больше из следующих статей –

• Экспоненциальное распределение
• эксцесс
• Эмпирическое правило