Линия наилучшего соответствия

Линия определения наилучшего соответствия

Линия наилучшего соответствия — это математическое понятие, которое связывает точки, разбросанные по графику. Это форма линейной регрессии, в которой используются данные разброса для определения наилучшего способа определения взаимосвязи между точками.

Концепция позволяет визуализировать собранные данные. При этом упрощается интерпретация данных.

Оглавление

• Линия определения наилучшего соответствия
  • Понимание линии наилучшего соответствия
  • Почему в исследованиях используется линия наилучшего соответствия?
  • Как рассчитать линию наилучшего соответствия?
  • Линия примеров наилучшего соответствия
  • Часто задаваемые вопросы (FAQ)
  • Рекомендуемые статьи

Ключевые выводы

• Линия наилучшего соответствия демонстрирует корреляцию между различными точками сетки.
• Его можно использовать для поиска тенденций путем определения взаимосвязи между различными точками на графике. Он широко используется на финансовом рынке и в научном мире.
• Для расчета используется следующая формула: Y = C +B¹(x¹) + B²(x²)

Понимание линии наилучшего соответствия

Линия наилучшего соответствия, также известная как регрессионно-регрессионный анализ, представляет собой статистический подход к оценке взаимосвязи между 1 зависимой переменной и 1 или более независимыми переменными. Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читать далее строку. По сути, это линия, которая показывает тенденции, за которыми следуют точки на сетке. Он используется для интерпретации визуального представления данных. Эта концепция помогает понять корреляцию между одной точкой и другой. Линия не так важна, как используемые данные. Это всего лишь инструмент, позволяющий визуализировать собранные данные.

Этот метод определяет, являются ли собранные данные линейными или нет. Чем линейнее данные, тем легче будет провести линию. Кроме того, линия более прямая, если данные линейны. Напротив, для коррелированной информации, включающей несколько источников, линия изогнута.

Почему в исследованиях используется линия наилучшего соответствия?

Эта концепция может быть полезна в нескольких контекстах. Один из них заключается в установлении связи между различными переменными. Установив эту взаимосвязь, можно выявить тенденции, которые без нее были бы затруднены. В результате этот метод используется в нескольких различных областях, таких как финансовый рынок и наука.

На финансовом рынке Финансовый рынок Термин «финансовый рынок» относится к рынку, на котором происходят такие действия, как создание и торговля различными финансовыми активами, такими как облигации, акции, товары, валюты и производные инструменты. Он предоставляет платформу для взаимодействия продавцов и покупателей и торговли по цене, определяемой рыночными силами. Более того, он используется для анализа собранных рыночных данных. Например, можно взять переменные из данных Nasdaq или данных о занятости в США за последние десять лет. Сопоставив данные и используя эту концепцию, можно лучше понять, как эти темы соотносятся друг с другом. Затем эта концепция используется для прогнозирования будущих тенденций с участием обеих переменных.

Рассмотрим еще один пример из науки. В геолого-геофизических исследованиях линия регрессии Линия регрессииЛиния регрессии указывает на линейную зависимость между зависимыми переменными по оси Y и независимыми переменными по оси X. Корреляция устанавливается путем анализа структуры данных, образованной переменными. Читать далее используется для нахождения взаимосвязей между несколькими переменными, связанными с Землей. При этом ученые лучше понимают историю планеты и предсказывают естественные проблемы.

Однако важно отметить, что эта концепция не дает автоматической корреляции между данными. Если заданные данные вообще не имеют отношения, то линию все равно можно вычислить, но это будет не очень полезно. Чтобы получить лучшие результаты, исследователям необходимо проанализировать данные независимо и посмотреть, имеют ли они смысл.

Как рассчитать линию наилучшего соответствия?

Самый простой способ рассчитать линию наилучшего соответствия — использовать программное обеспечение для регрессионного анализа. Однако важно выяснить логику процесса, чтобы понять, что делает компьютер. Изучив метод, любой может вычислить его, используя только лист бумаги и карандаш.

Сначала нанесите собранные данные на точечный график. Это важно, потому что устанавливает и упорядочивает значения, необходимые для формулы. Для расчета линии наилучшего соответствия используется следующая формула:

Y = C + B¹(x¹) + B²(x²)

Здесь, Д является зависимой переменной уравнения.

• С постоянна.
• B¹ и B² — первый и второй коэффициенты регрессии.
• X¹ и X² — первая и вторая независимые переменные. или финансовое моделирование.Подробнее.

Прежде чем вычислять формулу, исследователям необходимо понять соответствующие значения на графике. Рассмотрим финансовый пример, приведенный ранее: корреляция Nasdaq с десятью годами занятости в США. Если исследователи смогут выбирать образцы из четырех наборов данных в течение каждого года, у них будет 40 различных точек.

В этом случае цена акций будет постоянной, тогда как цены Nasdaq и уровень занятости будут другими независимыми переменными. Найдя результаты, исследователи смогут подвести черту.

Линия примеров наилучшего соответствия

Рассмотрим следующие примеры, чтобы лучше понять, как должна располагаться линия и что она означает.

В первом примере легко определить линию, потому что результаты относительно линейны. Как правило, это показывает преемственность того, что ищет исследователь.

Однако во втором примере можно понять, как изменится график, если одна из точек окажется чуть ниже регрессии. Даже одна точка может потянуть всю строку вниз. Несмотря на то, что одна точка данных находится за пределами линии, общий результат все еще довольно линейный.

Третий пример ясно демонстрирует, что можно провести прямую регрессивную линию, даже если результаты будут менее линейными. Это когда эта математическая концепция действительно полезна, потому что она показывает идеальную линию среди данных, которые не являются полностью линейными. Без использования этого метода было бы трудно интерпретировать данные.

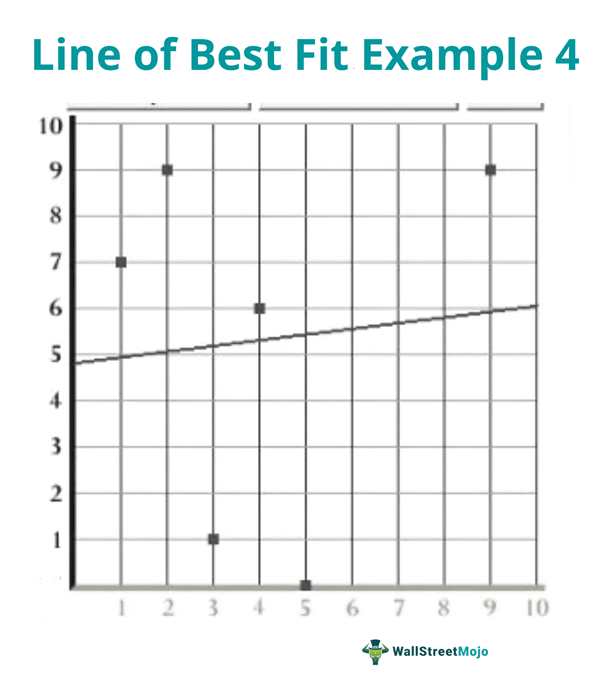
В четвертом примере линия была нарисована на основе расчета, но на самом деле она ничего не представляет. Это происходит, когда данные на самом деле не коррелированы. Когда между точками данных нет связи, этот метод не может найти новую связь.

Часто задаваемые вопросы (FAQ)

Что понимается под линией наилучшего соответствия?

Это математическая концепция, которая связывает точки, разбросанные по графику. Это форма линейной регрессии, в которой используются данные разброса для определения наилучшего способа определения взаимосвязи между точками.

Для чего используется линия хорошей посадки?

Это понятие используется в процедурах прогнозирования. Его цель — описать взаимосвязь зависимой переменной (переменной у) с одной или многими независимыми переменными (переменной х).

Является ли линия регрессии линией хорошего соответствия?

Линия регрессии иногда называется «линией наилучшего соответствия», потому что это линия, которая лучше всего подходит, если провести ее через точки. Это линия, которая минимизирует расстояние фактических результатов от прогнозируемых результатов.

Рекомендуемые статьи

Это руководство по линии наилучшего соответствия и ее определению. Здесь мы обсудим, как его рассчитать, а также его использование, графики и примеры. Вы можете узнать больше о финансировании из следующих статей –

• Регрессия методом наименьших квадратов
• Примеры линейной регрессии
• Нелинейная регрессия в Excel