Функция плотности вероятности

Что такое функция плотности вероятности?

Функция плотности вероятности дает результат, указывающий плотность непрерывной случайной величины, лежащей между определенным диапазоном значений. Если данный сценарий рассчитывается на основе чисел и значений, функция вычисляет плотность, соответствующую указанному диапазону.

Функция при решении определяет связь между случайной величиной и ее вероятностью. Вероятность переменной сопоставляется при решении функции. Функция обозначается f(x), а графическое изображение дает кривую нормального распределения. Площадь между любыми двумя конкретными значениями дает вероятность исхода указанного наблюдения.

Оглавление

• Что такое функция плотности вероятности?
  • Объяснение функции плотности вероятности
    • #1 – Дискретная переменная
    • #2 – Непрерывная переменная
  • Формула
  • Примеры с расчетом
  • Приложения
  • Часто задаваемые вопросы (FAQ)
  • Рекомендуемые статьи

Ключевые выводы

• Функция плотности вероятности (PDF) дает результат, указывающий плотность непрерывной случайной величины, лежащей между определенным диапазоном значений.
• Императивно существует два типа переменных: дискретные и непрерывные. PDF превращается в функцию массы вероятности при работе с дискретными переменными.
• Он используется в статистических расчетах и ​​графически представляется в виде колоколообразной кривой, формирующей связь между переменной и ее вероятностью.
• Его применение важно в алгоритмах машинного обучения, аналитике, теории вероятностей, нейронных сетях и т. д.

Объяснение функции плотности вероятности

Функция плотности вероятности (PDF) связана с непрерывной случайной величиной путем нахождения вероятности, попадающей в определенный интервал. Непрерывная случайная величина может принимать несчетно бесконечное число возможных значений. Функция массы вероятности заменяет PDF для дискретной случайной величины, которая принимает конечные или счетные возможные значения.

PDF-файлы имеют широкий спектр приложений. Например, он используется при моделировании и прогнозировании, связанных с химически реактивными турбулентными потоками, а также при анализе доходности акций. Для каждого приложения соответствующая кривая изображается на графике, а анализ характеристик кривой колокола, таких как симметрия и стороны, такие как левая или правая, дает важную информацию.

Еще одним важным понятием, важным для понимания PDF, является кумулятивная функция распределения. Он также используется для объяснения распределения случайных величин, в первую очередь непрерывных случайных величин. Дифференцирующая кумулятивная функция распределения непрерывной случайной величины даст значение PDF, а интегрирование PDF даст значение кумулятивной функции распределения.

Формула

Формула функции плотности вероятности:

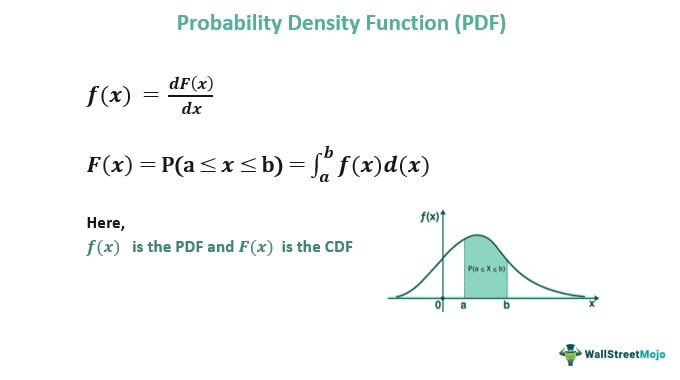
Для расчета функции плотности вероятности PDF онлайн калькулятор или формула на основе кумулятивной функции распределения используется, мы дифференцируем кумулятивную функцию распределения:

f(x) — PDF, а F(x) — CDF

или

Здесь,

• X лежит между нижним пределом «а» и верхним пределом «b»
• F(b): Кумулятивная функция распределения при
• F(a): кумулятивная функция распределения в точке b

Примеры с расчетом

Чтобы лучше понять формулу и ее применение, рассмотрите следующий пример PDF:

ПДФ это:

Найти P(1

Формула:

Применение верхнего и нижнего пределов:

Приложения

• Используется в алгоритмах машинного обучения, аналитике, теории вероятностей, нейронных сетях и т.д.
• Вычисляет вероятности, связанные с непрерывными случайными величинами.
• PDF доходности цен на акции используется для изучения различных рыночных сценариев.
• Он используется для моделирования различных процессов и получения решений проблемы. Например, применяется к моделировать химически реагирующие турбулентные потоки и получить соответствующее решение проблем закрытия.

Часто задаваемые вопросы (FAQ)

Какова формула функции плотности вероятности?

е(х) это PDF и Ф(х) это CDF
или

Здесь,
· X лежит между нижним пределом ‘a’ и верхним пределом ‘b’
· F(b): кумулятивная функция распределения при
· F(a): Кумулятивная функция распределения в точке b

Что такое совместная функция плотности вероятности?

Функция, совместная PDF, обозначает распределение вероятностей двух или более непрерывных случайных величин, которые вместе образуют непрерывный случайный вектор. Если две случайные величины имеют совместную PDF, они совместно непрерывны. Его вычисление связано с применением нескольких интегралов.

Что такое пример функции плотности вероятности?

Рассмотрим пример с PDF, f(x) = x + 3, когда 1 < x ≤ 3. Нам нужно найти P(2 < X < 3). Интегрирование x + 3 в пределах 2 и 3 дает ответ 5.5.

Рекомендуемые статьи

Это руководство о том, что такое функция плотности вероятности (PDF) и ее определение. Мы объясняем формулы, расчеты, приложения, примеры и совместный PDF. Вы можете узнать больше из следующих статей –

• Апостериорная вероятность
• Условная возможность
• Априорная вероятность