Формула R в квадрате

Что такое R в квадрате (R2) в регрессии?

R-квадрат (R2) является важным статистическим показателем. Модель регрессии представляет долю разницы или дисперсии в статистических терминах для зависимой переменной, которую может объяснить независимая переменная или переменные. Короче говоря, он определяет, насколько хорошо данные будут соответствовать регрессионной модели.

Оглавление

• Что такое R в квадрате (R2) в регрессии?
  • Формула R в квадрате
  • Объяснение
  • Примеры
  • Актуальность и использование
  • Рекомендуемые статьи

Формула R в квадрате

Чтобы рассчитать R-квадрат, вам нужно определить коэффициент корреляции, а затем возвести результат в квадрат.

Формула R в квадрате = r2

Где r коэффициент корреляции можно рассчитать, как показано ниже:

р = п (∑ху) – ∑х ∑у / √ [n* (∑x2 – (∑x)2)] * [n* (∑y2 – (∑y)2)]

Где,

• r = коэффициент корреляции
• n = число в данном наборе данных
• x = первая переменная в контексте
• у = вторая переменная

Объяснение

Предположим, что между этими двумя переменными существует какая-либо связь или корреляция, которая может быть линейной или нелинейной. В этом случае, если происходит изменение значения независимой переменной, значение другой зависимой переменной, вероятно, изменится, скажем, линейно или нелинейно.

Часть формулы в числителе проверяет, двигаются ли они вместе и удаляют ли они свои движения. Относительная сила их обоих, движущихся вместе. Часть формулы в знаменателе масштабирует числитель, используя квадратный корень из произведения разностей между переменными и их переменных в квадрате. И когда вы возводите этот результат в квадрат, мы получаем R-квадрат, который представляет собой не что иное, как коэффициент детерминации. Коэффициент детерминацииКоэффициент детерминации, также известный как R в квадрате, определяет степень дисперсии зависимой переменной, которую можно объяснить независимой переменной . Следовательно, чем выше коэффициент, тем лучше уравнение регрессии, так как это означает, что независимая переменная выбрана с умом. Подробнее.

Примеры

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel с формулой R в квадрате здесь – Шаблон Excel с формулой R в квадрате

Пример №1

Рассмотрим следующие две переменные x и y, необходимые для расчета R в квадрате в регрессии.

Решение:

Используя формулу, упомянутую выше, нам нужно сначала рассчитать коэффициент корреляцииРассчитать коэффициент корреляцииКоэффициент корреляции, иногда называемый коэффициентом взаимной корреляции, представляет собой статистическую меру, используемую для оценки силы взаимосвязи между двумя переменными. Его значения варьируются от -1,0 (отрицательная корреляция) до +1,0 (положительная корреляция). читать далее.

У нас есть все значения в приведенной выше таблице с n = 4.

Давайте теперь введем значения формул, чтобы получить фигуру.

г = (4 * 26 046,25) – (265,18 * 326,89)/ √ [(4 * 21,274.94) – (326.89)2] * [(4 * 31,901.89) – (326.89)2]

г = 17 501,06 / 17 512,88

Коэффициент корреляции будет-

г = 0,99932480

Итак, расчет будет следующим:

г2 = (0,99932480)2

Формула R в квадрате в регрессии

г2 = 0,998650052

Пример #2

Индия, развивающаяся страна, хочет провести независимый анализ того, повлияли ли изменения цен на сырую нефть на ее стоимость в рупии. Ниже приводится история цены сырой нефти марки Brent и курса рупии по отношению к доллару, который преобладал в среднем в последующие годы.

Решение:

Используя приведенную выше формулу для корреляции, мы можем сначала вычислить коэффициент корреляции. Рассматривая среднюю цену сырой нефти как одну переменную, скажем, x, и рассматривая рупию за доллар как другую переменную как y.

RBI, Центральный банк Индии, обратился к вам с просьбой представить презентацию на следующей встрече. Но сначала определите, влияет ли движение сырой нефти на движение рупии за доллар.

Решение:

Используя приведенную выше формулу для корреляции, мы можем сначала вычислить коэффициент корреляции. Например, рассматривая среднюю цену сырой нефти как одну переменную, скажем, x, и рассматривая рупию за доллар как другую, как y.

У нас есть все значения в приведенной выше таблице с n = 6.

Давайте теперь введем значения формул, чтобы получить фигуру.

Коэффициент корреляции будет-

г = (6 * 23592,83) – (356,70 * 398,59) / √ [(6 * 22829.36) – (356.70)2] * [(6 * 26529.38) – (398.59)2]

г = -620,06 / 1715,95

г = -0,3614

Итак, расчет будет следующим:

г2 = (-0,3614)2

Формула R в квадрате в регрессии

г2 = 0,1306

Анализ: Существует незначительная связь между изменениями цен на сырую нефть и ценой индийской рупии. По мере роста цен на сырую нефть также сказываются изменения курса индийской рупии. Но поскольку R-квадрат составляет всего 13%, изменения цен на сырую нефть очень мало объясняют изменения курса индийской рупии. Индийская рупия также подвержена изменениям других переменных, которые необходимо учитывать.

Пример №3

Лаборатория XYZ исследует рост и вес и интересуется, есть ли связь между этими переменными. Собрав выборку из 5000 человек для каждой категории, мы определили средний вес и рост в этой конкретной группе.

Ниже приведены детали, которые они собрали.

Вам необходимо рассчитать R-квадрат и сделать вывод, объясняет ли эта модель, что различия в росте влияют на различия в весе.

Решение:

Используя приведенную выше формулу для корреляции, мы можем сначала вычислить коэффициент корреляции. Например, рассматривая рост как одну переменную, скажем, x, а вес как другую, как y.

У нас есть все значения в приведенной выше таблице с n = 6.

Давайте теперь введем значения в формулу, чтобы получить цифру.

г = (7 * 74 058,67) – (1031 * 496,44) / √[(7 * 153595 – (1031)2] * [(7 * 35793.59) – (496.44)2]

г = 6 581,05 / 7 075,77

Коэффициент корреляции будет-

Коэффициент корреляции (r) = 0,9301

Итак, расчет будет следующим:

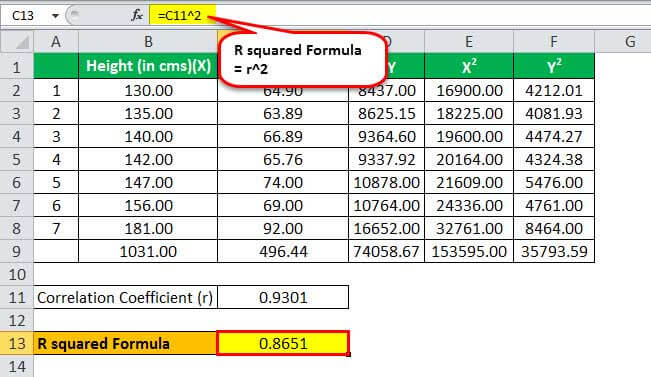
г2 = 0,8651

Анализ: Корреляция положительная. Оказывается, есть некоторая связь между ростом и весом. По мере увеличения роста увеличивается и вес человека. В то время как R2 предполагает, что 86% изменений в росте связаны с изменениями в весе, 14% необъяснимы.

Актуальность и использование

Актуальность R-квадрата в регрессии заключается в его способности находить вероятность будущих событий, происходящих в пределах заданных прогнозируемых результатов или исходов. Если в модель добавить больше выборок, коэффициент покажет вероятность или вероятность того, что новая точка или новый набор данных попадут на линию. Определение не доказывает причинно-следственную связь, даже если обе переменные имеют сильную связь.

Некоторые из областей, где R в квадрате в основном используется для отслеживания взаимных фондовВзаимный фондВзаимный фонд — это профессионально управляемый инвестиционный продукт, в котором пул денег от группы инвесторов инвестируется в активы, такие как акции, облигации и т. д.Читать больше производительность, отслеживание риск в хедж-фондах и определение того, насколько хорошо акции движутся вместе с рынком, где R2 предполагает, какая часть акций может быть объяснена движениями на рынке.

Рекомендуемые статьи

Эта статья была руководством по формуле R-квадрата в регрессии. Здесь мы узнаем, как рассчитать R-квадрат, используя его формулу, примеры и загружаемый шаблон Excel. Вы можете узнать больше о финансовом анализе из следующих статей:

• Скорректированный R в квадрате Скорректированный R в квадрате Скорректированный R в квадрате относится к статистическому инструменту, который помогает инвесторам измерять степень дисперсии зависимой переменной, которая может быть объяснена независимой переменной, и учитывает влияние только тех независимых переменных, которые имеют влияние на изменение зависимой переменной.Подробнее
• Формула корреляцииФормула корреляцииКорреляция — это статистическая мера между двумя переменными, которая определяется как изменение одной переменной, соответствующее изменению другой. Он рассчитывается как (x(i)-среднее(x))*(y(i)-среднее(y)) / ((x(i)-среднее(x))2 * (y(i)-среднее( у))2.Подробнее
• Формула регрессии
• ПримерыПримерыЛинейная регрессия представляет отношение между одной зависимой переменной и одной или несколькими независимыми переменными. Примерами линейной регрессии являются взаимосвязь между ежемесячными продажами и расходами, уровнем IQ и результатами тестов, ежемесячными температурами и продажами кондиционеров, населением и мобильными продажами. Подробнее о линейной регрессии