Тотиентная функция Эйлера
Что такое Тотиентная функция Эйлера?
Общая функция Эйлера — это математическая мультипликативная функция, которая подсчитывает положительные целые числа до заданного целого числа, обычно называемого «n», которое является простым числом до «n». Можно использовать эту функцию, чтобы узнать количество простых чисел, которые существуют до заданного целого числа n.
Искусственный интеллект поможет тебе заработать!
Оглавление
Объяснение
Тотальную функцию Эйлера можно использовать, чтобы узнать, сколько простых чисел подходит к заданному целому числу n. Ее также называют арифметической функцией. Две вещи важны для приложения или использования функции Эйлера totient. Во-первых, НОД, образованный из заданного целого числа «n», должен быть мультипликативным. Во-вторых, числа gcd должны быть только простыми числами. Целое число n в этом случае должно быть больше 1. Вычисление общей функции Эйлера из отрицательного целого числа невозможно. Принцип в этом случае состоит в том, что для ϕ(n) мультипликаторы с именами m и n должны быть больше 1. Следовательно, обозначается как 1 Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:) Эйлер ввел эту функцию в 1763 году. Первоначально Эйлер использовал греческую Пи для обозначения функции, но из-за некоторых проблем его обозначение греческого π не получить признание. И он не смог дать ему правильный знак записи, т. е. ϕ. Следовательно, он не может ввести функцию. Кроме того, ϕ был взят из «Арифметических исследований» Гаусса 1801 года. Эта функция также известна как фи-функция. Но Дж. Дж. Сильвестр в 1879 году включил термин totient для этой функции из-за ее свойств и использования. Различные правила имеют дело с различными типами целых чисел, например, если целое число p является простым числом, то какое правило следует применять и т. д. Эйлер формулирует все правила как практически выполнимые. Поэтому его можно использовать и сегодня, имея дело с тем же самым. Есть несколько разных свойств. Некоторые из свойств тотиентной функции Эйлера: Φ(mn) = ϕ(m) * ϕ(n) (1- 1/m) (1 – 1/ n) Пример №1 Рассчитать ϕ (7)? Решение: ф ( 7 ) = (1,2,3,4,5,6) = 6 Поскольку все числа являются простыми до 7, это упростило вычисление ϕ. Пример #2 Рассчитать ϕ ( 100 )? Решение: Поскольку 100 — большое число, требуется много времени, чтобы вычислить от 1 до 100 простых чисел, которые являются простыми числами со 100. Следовательно, мы применяем следующую формулу: Пример №3 Рассчитать ϕ (240)? Число, кратное 240, равно 16*5*3, т.е. 2 4 * 5 * 3. если nM не является простым числом, мы используем nm – nm-1 Пример №4 Рассчитать ϕ ( 49 )? Различные приложения, как показано ниже: Тотиентная функция Эйлера полезна во многих отношениях. Его можно использовать в системе шифрования RSA в целях безопасности. Функция имеет дело с теорией простых чисел, а также полезна при расчете больших вычислений. Эту функцию также можно использовать в алгебраических вычислениях и элементарных числах. Для обозначения функции используется символ ϕ, также называемый фи-функцией. Функция состоит больше из теоретического использования, а не практического использования. Практическое использование функции ограничено. Функцию можно понять на различных практических примерах, а не на теоретических объяснениях. Существуют разные правила вычисления функции Эйлера, и к разным числам применяются разные правила. Впервые функция была введена в 1763 году. Из-за некоторых проблем она получила признание в 1784 году, а название было изменено в 1879 году. Функция универсальна и может применяться повсеместно. Эта статья была руководством по функции Тотиента Эйлера. Здесь мы обсуждаем вычисление тотиентной функции Эйлера, примеры и приложения. Вы можете узнать больше о финансировании из следующих статей: – Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)История
Свойства функции Тотиента Эйлера
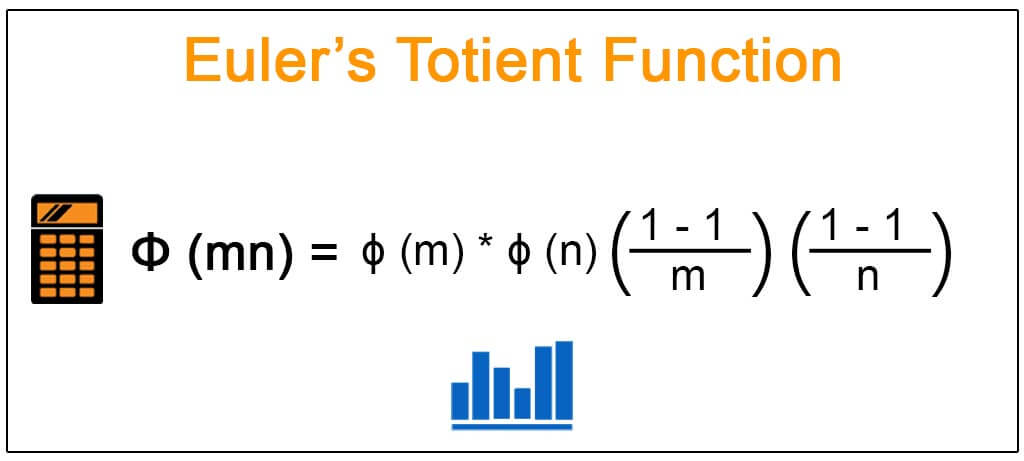
Вычислите функцию Эйлера Тотиент
Приложения
Заключение
Рекомендуемые статьи