Зависимая переменная

Что такое зависимая переменная?

Зависимая переменная — это переменная, значение которой изменяется в ответ на изменение значения независимой переменной. Это результат эксперимента или статистического анализа; следовательно, также называется левой переменной, обычно представленной как «Y» на графике.

Отношения между независимыми и зависимыми переменными означают причинно-следственный феномен, когда любое изменение значения первой вызывает изменение значения второй.

Оглавление

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

Что такое зависимая переменная?

Зависимая переменная — это фактор, событие или значение, которое изменяется при изменении другой переменной (независимой переменной). Его также называют левосторонним результатом или переменной отклика.
На графике левая переменная отмечена на вертикальной линии, т. е. на оси y, и математически обозначена как y = f(x).
Это одна из двух важнейших переменных любого исследования, т. е. научных экспериментов, проверки гипотез, статистического анализа или математических рассуждений.
Также зависимая переменная в одном случае может быть независимой переменной в другом исследовании.

Зависимая переменная объяснила

Зависимой переменной может быть что угодно, событие, значение или объект, возникновение изменения которого зависит от изменения независимой переменной. Для графического представления независимая переменная указывается как значение x. Это потому, что он отображается на горизонтальной линии — оси x. Переменная результата, с другой стороны, представлена как значение y на вертикальной линии — оси y. Таким образом, переменная отклика может быть математически записана как:

у = е (х)

В научных экспериментах, статистике, проверке гипотез и математических рассуждениях результаты (значения переменных результата) интерпретируются путем подстановки значений независимых переменных в уравнение, которое связывает две переменные.

Кроме того, исследователь может подставлять различные значения X, чтобы получить желаемую переменную отклика, т. е. Y. Анализ также определяет степень отклонения переменной результата — когда независимая переменная изменяется. Зависимые и независимые переменные подобны двум сторонам медали и незаменимы в исследованиях, анализе и науке. В то время как переменная результата является следствием, независимая переменная является его причиной.

Важно отметить, что переменная результата одного исследования может действовать как
независимая переменная для другого. Например, высокие производственные затраты приводят к более низкой марже прибыли. Маржа прибыли Маржа прибыли — это показатель, который руководство, финансовые аналитики и инвесторы используют для измерения прибыльности бизнеса по отношению к его продажам. Он определяется как отношение суммы сгенерированной прибыли к сумме сгенерированного дохода. читать дальше для компании. Снижение маржи прибыли приводит к убыткам компании. Здесь более низкая норма прибыли является переменной отклика в первом сценарии, но независимой переменной во втором.

Переменная результата — это та переменная, изменение которой исследуется путем изменения входных данных; в статистических условиях они называются регрессорами. Стабильность отличает более качественные переменные. Воздействие на переменную не должно меняться при повторении — с теми же участниками, условиями и экспериментальными манипуляциями.

В реальных приложениях операционализация переменных очень важна. Проще говоря, это относится к методам измерения: полезная переменная — это та, которую можно измерить.

График

Анализ исследования можно изобразить на графике, если известны переменные результата и независимые переменные. Независимые переменные помещаются в данное уравнение для получения результата или переменной результата:

Y = а + bX

Здесь,
«Y» — зависимая переменная;
‘a’ – точка пересечения Y;
«Х» — независимая переменная; и
«b» — это коэффициент или наклон.

На графике эти переменные представлены следующим образом:

Зависимые переменные отмечены на оси Y.
Независимые переменные отображаются на оси x.

Предположим, что у нас есть регрессия. Регрессия. Регрессионный анализ — это статистический подход для оценки взаимосвязи между 1 зависимой переменной и 1 или более независимыми переменными. Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг. читать далее уравнение Y = 12 – 2X. Значения переменных результата и независимых переменных приведены ниже:

Y = 12 – 2X

12 – 2 × 1 = 10
12 – 2 × 2 = 8
12 – 2 × 3 = 6
12 – 2 × 4 = 4
12 – 2 × 5 = 2

Теперь давайте нанесем приведенные выше данные на график регрессии:

Примеры

Давайте рассмотрим несколько примеров, чтобы проследить корреляцию между независимыми переменными и переменными результата:

Пример 1

План взаимных фондов обеспечивает более высокую прибыль, когда 10 000 долларов инвестируются на более длительный период. Ниже показано увеличение доходов, вызванное увеличением продолжительности инвестиций:

Инвестиционный период Расчетный доход
1 год – $1200
2 года — $2544
3 года — 4049 долларов
4 года — 5735 долларов США
5 лет — $7623

В приведенном выше примере период инвестирования является независимой переменной, а предполагаемая доходность — переменной результата. Теперь изобразим это на графике:

На приведенном выше графике мы видим, что увеличение предполагаемой доходности зависит от периода инвестирования.

Пример 2

Существует зависимость между спросом, предложением и ценой товара. Цена товара зависит от спроса и предложения на рынке.

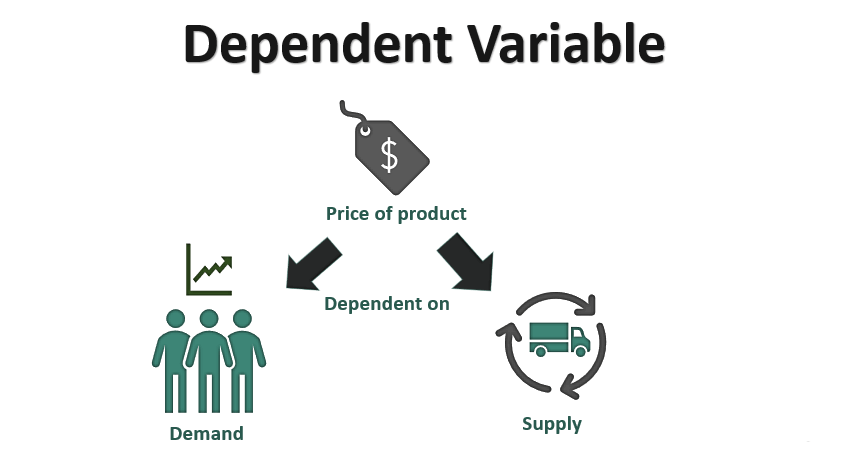
Здесь цена является зависимой переменной; он будет реагировать на изменения независимых факторов, т. е. спроса и предложения продукта.

Часто задаваемые вопросы (FAQ)

В чем разница между зависимыми и независимыми переменными?

Переменная результата относится к событию или значению, возникновение или изменение которого зависит от изменения другой переменной — независимой переменной. Напротив, независимая переменная — это та, которая возникает или значение которой изменяется само по себе без влияния других факторов.

Независимая переменная влияет на переменную результата. Когда исследователь изменяет независимую переменную, записывается ее влияние на переменную результата.

Что является примером зависимой переменной?

Для экзамена измеряются результаты тестов; здесь результаты тестов являются зависимыми переменными. Результат зависит от обучения, поэтому действует как независимая переменная. Репетиторство является независимым; наблюдается влияние смены наставников и стиля обучения на результаты тестов.

Как определить независимые и зависимые переменные?

Между независимыми и зависимыми переменными существует причинно-следственная связь; таким образом, если одна переменная запускает другую или влияет на нее, это независимая переменная. Однако другая переменная будет результатом этого влияния, что показывает, что она является зависимой переменной, также известной как переменная результата.

Зависимая переменная

Что такое зависимая переменная?