Формула нормального распределения

Нормальное распределение симметрично, т. е. положительные и отрицательные значения распределения можно разделить на равные половины; следовательно, среднее значение, медиана и мода будут равны. У него два хвоста. Один известен как правый хвост, а другой известен как левый хвост.

Формула для расчета выглядит следующим образом:

X ~ N (µ, α)

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

Где

N = количество наблюдений
µ = среднее значение наблюдений
α = стандартное отклонение

В большинстве случаев наблюдения мало что раскрывают в необработанном виде. Таким образом, важно стандартизировать наблюдения, чтобы сравнить это. Это можно сделать с помощью формулы z-оценкиФормула Z-оценкиZ-оценка необработанных данных относится к оценке, полученной путем измерения того, сколько стандартных отклонений выше или ниже совокупности означает данные, что помогает проверить рассматриваемую гипотезу. Другими словами, это расстояние точки данных от среднего значения генеральной совокупности, которое выражается как кратное стандартному отклонению. Подробнее. Требуется рассчитать Z-оценку для наблюдения.

Уравнение для расчета Z-показателя для нормального распределения выглядит следующим образом:

Z=(X- µ)/ а

Где

Z = Z-оценка наблюдений
µ = среднее значение наблюдений
α = стандартное отклонение

Оглавление

Формула нормального распределения

Объяснение

Распределение является нормальным, когда оно следует колоколообразной кривой. График колоколообразной кривой изображает нормальное распределение, которое является типом непрерывной вероятности. Он получил свое название из-за формы графика, напоминающего колокол. читать далее. Она известна как кривая колокола, так как принимает форму колокола. Одной из наиболее важных характеристик нормальной кривой является то, что она симметрична, что означает, что положительные и отрицательные значения распределения можно разделить на равные половины. Еще одна важная характеристика переменной заключается в том, что наблюдения будут находиться в пределах 1 стандартного отклонения от среднего значения в 90% случаев. Наблюдения будут иметь два стандартных отклонения от среднего значения в 95% случаев и в пределах трех стандартных отклонений от среднего значения в 99% случаев.

Примеры

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон Excel формулы нормального распределения здесь – Шаблон Excel с формулой нормального распределения

Пример №1

Средний вес класса студентов составляет 65 кг, а стандарт веса – 0,5 кг. Если считать, что распределение отдачи нормальное, то интерпретируем для веса учащихся в классе.

Когда распределение нормальное Распределение нормальное Нормальное распределение представляет собой колоколообразную кривую частотного распределения, которая помогает описать все возможные значения, которые случайная величина может принимать в заданном диапазоне, при этом большая часть области распределения находится в середине, а небольшая часть — в хвостах. крайности. Это распределение имеет два ключевых параметра: среднее значение (µ) и стандартное отклонение (σ), которое играет ключевую роль в расчете доходности активов и в стратегии управления рисками. Читать далее, 68% из них лежат в пределах 1 стандартного отклонения, 95% находится в пределах 2 стандартных отклонений, а 99% лежит в пределах 3 стандартных отклонений.

Данный,

Средняя отдача от веса составит 65 кг.
Стандартное отклонение составит 3,5 кг.

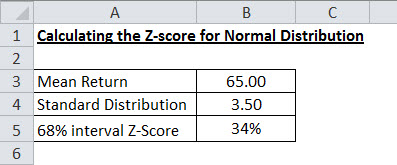
Таким образом, в 68% случаев значение распределения будет находиться в диапазоне ниже,

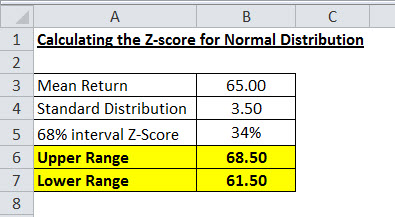
Верхний диапазон = 65+3,5= 68,5
Нижний диапазон = 65-3,5= 61,5
Каждый хвост будет (68%/2) = 34%

Пример #2

Продолжим на том же примере. Средний вес класса студентов составляет 65 кг, а стандарт веса – 3,5 кг. Если предположить, что распределение отдачи нормальное, то интерпретируем его для веса учащихся в классе.

Данный,

Средняя отдача от веса составит 65 кг.
Стандартное отклонение составит 3,5 кг.

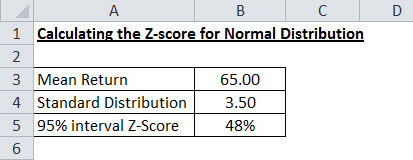
Таким образом, в 95% случаев значение распределения будет находиться в диапазоне, как показано ниже:

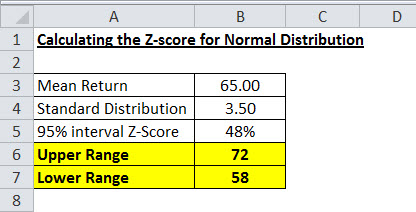
Верхний диапазон = 65 + (3,5 * 2) = 72
Нижний диапазон = 65-(3,5*2)= 58
Каждый хвост будет (95%/2) = 47,5%

Пример №3

Продолжим на том же примере. Средний вес класса учащихся составляет 65 кг, а стандарт веса – 3,5 кг. Если предположить, что распределение отдачи нормальное, то интерпретируем его для веса учащихся в классе.

Данный,

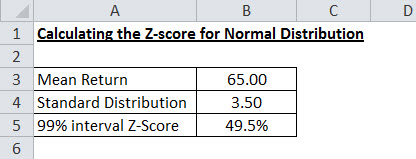
Средняя отдача от веса составит 65 кг.
Стандартное отклонение составит 3,5 кг.

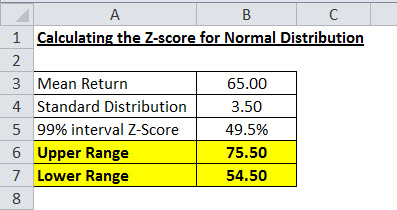
Таким образом, в 99% случаев значение распределения будет находиться в диапазоне, как показано ниже:

Верхний диапазон = 65+(3,5*3)= 75,5
Нижний диапазон = 65-(3,5*3)= 54,5
Каждый хвост будет (99%/2) = 49,5%

Актуальность и использование

Нормальное распределение является важной статистической концепцией, поскольку большинство случайных величин в финансах следуют такой кривой. Он играет важную роль в построении портфолио. Помимо финансов, за таким распределением должно следовать множество реальных параметров. Например, если мы попытаемся найти рост учеников в классе или вес учеников, наблюдения будут нормально распределены. Точно так же и оценки за экзамен следуют тому же распределению. Это помогает нормализовать оценки на экзамене, если большинство студентов набрали меньше проходного балла, установив ограничение на высказывание только тех, кто не сдал экзамен и набрал меньше двух стандартных отклонений.