Формула экстраполяции

Определение формулы экстраполяции

Формула экстраполяции — это формула, используемая для оценки значения зависимой переменной относительно независимой переменной, которая должна лежать в диапазоне за пределами данного набора данных. Например, точно известен расчет линейного исследования с использованием двух конечных точек (x1, y1) и (x2, y2) на линейном графике, когда значение экстраполируемой точки равно «x», формула, которую можно использовать представляется как y1+ [(x−x1) / (x2−x1)] *(у2-у1).

Оглавление

Определение формулы экстраполяции

Y(x) = Y(1)+ (x-x(1)/x(2)-x(1)) * (Y(2) – Y(1))

Программы для Windows, мобильные приложения, игры - ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале - Подписывайтесь:)

Расчет линейной экстраполяции (шаг за шагом)

Формулу линейной экстраполяции можно разделить на следующие шаги:

Во-первых, необходимо проанализировать данные, чтобы определить, следуют ли данные за тенденцией и можно ли прогнозировать то же самое.
Должно быть две переменные: одна должна быть зависимой переменной, а вторая должна быть независимой переменной.
Числитель формулы начинается с предыдущего значения зависимой переменной. Затем нужно добавить долю независимой переменной при расчете среднего значения для интервалов классов.
Наконец, умножьте значение, полученное на шаге 3, на разницу непосредственно заданных зависимых значений. Добавление шага 4 к значению зависимой переменной даст экстраполированное значение.

Примеры

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%} Вы можете скачать этот шаблон формулы экстраполяции Excel здесь – Формула экстраполяции Шаблон Excel

Пример №1

Предположим, что значение некоторых переменных приведено ниже в виде (X, Y):

(4, 5)
(5, 6)

Основываясь на приведенной выше информации, вы должны найти значение Y(6), используя метод экстраполяции.

Решение

Используйте приведенные ниже данные для расчета.

Х1: 4,00
Y2: 6.00
Y1: 5,00
Х2: 5,00

Расчет Y(6) по формуле экстраполяции выглядит следующим образом:

Экстраполяция Y(x) = Y(1) + (x) – (x1) / (x2) – (x1) x {Y(2) – Y(1)}

Y(6) = 5 + 6 – 4 / 5 – 4 х (6 – 5)

Ответ будет –

Y3 = 7

Следовательно, значение для Y, когда значение X равно 6, будет равно 7.

Пример #2

Г-н М и г-н Н являются учащимися 5-го стандарта, и в настоящее время они анализируют данные, предоставленные им их учителем математики. Учитель попросил их вычислить вес учеников, чей рост будет 5,90, и сообщил им, что приведенный ниже набор данных следует линейной экстраполяции.

ИксВысотаДМассаX15.00Y150X25.10Y252X35.20Y353X45.30Y455X55.40Y556X65.50Y657X75.60Y758X85.70Y859X95.80Y962

Предполагая, что эти данные следуют линейному ряду, вы должны рассчитать вес, который будет зависимой переменной Y в этом примере, когда независимая переменная x (рост) равна 5,90.

Решение

В этом примере нам теперь нужно узнать значение, или, другими словами, нам нужно спрогнозировать значение учащихся, чей рост равен 5,90, на основе тенденции, указанной в примере. Затем мы можем использовать приведенную ниже формулу экстраполяции в Excel для расчета веса, который является зависимой переменной для заданного роста и независимой переменной.

Расчет Y (5,90) выглядит следующим образом:

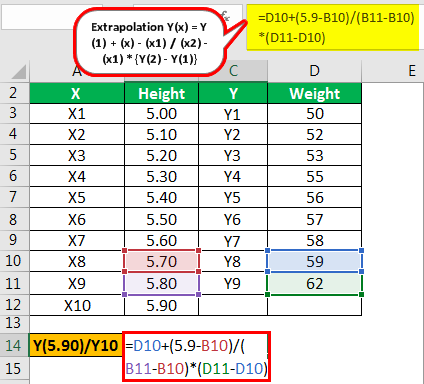
Экстраполяция Y(5.90) = Y(8) + (x) – (x8) /(x9) – (x8) x [Y(9) – Y(8)]
Y(5,90) = 59 + 5,90 – 5,70 / 5,80 – 5,70 х (62 – 59)

Ответ будет –

= 65

Следовательно, значение Y, когда значение X равно 5,90, будет равно 65.

Пример №3

Г-н В. является исполнительным директором компании ABC. Он был обеспокоен продажами компании после тенденции к снижению. Поэтому он попросил свой исследовательский отдел произвести новый продукт, который будет соответствовать растущему спросу по мере увеличения производства. Через 2 года они разработали продукт, спрос на который рос.

Ниже приведены подробности за последние несколько месяцев:

Х (Производство)Произведено (единиц)Y (спрос)Спрос (единиц)X110.0Y120.00X220.00Y230.00X330.00Y340.00X440.00Y450.00X550.00Y560.00X660.00Y670.00X770.00Y780.00X880.00Y890.00X990.00Y9100.00

Они заметили, что, поскольку изначально это был новый и дешевый продукт, спрос на него будет линейным до определенного момента.

Следовательно, продвигаясь вперед, они сначала прогнозируют спрос, а затем сравнивают его с фактическим и производят соответственно, поскольку это потребовало от них огромных затрат.

Менеджер по маркетингу хочет знать, что будет требоваться, если они произведут 100 единиц. Основываясь на приведенной выше информации, вы должны рассчитать спрос в единицах, когда они производят 100 единиц.

Решение

Мы можем использовать приведенную ниже формулу для расчета потребности в единицах, которая является зависимой переменной для данных произведенных единиц, которая является независимой переменной.

Расчет Y(100) выглядит следующим образом:

Экстраполяция Y(100) = Y(8) + (x) – (x8) / (x9) – (x8) x [ Y(9) – Y(8)]
Y(100) = 90 + 100 – 80 / 90 – 80 х (100 – 90)

Ответ будет –

= 110

Следовательно, значение для Y, когда значение X равно 100, будет равно 110.

Актуальность и использование

В основном используется для прогнозирования данных, выходящих за пределы текущего диапазона данных. В этом случае предполагается, что тенденция будет продолжаться для данных данных и даже за пределами этого диапазона, что не всегда так. Следовательно, следует осторожно использовать экстраполяцию. Вместо этого interpolationInterpolationInterpolation представляет собой математическую процедуру, применяемую для получения значения между двумя точками, имеющими заданное значение. Он аппроксимирует значение данной функции в заданном наборе дискретных точек. Его можно применять для оценки различных концепций стоимости, математики, статистики. Этот метод лучше подходит для того, чтобы сделать то же самое.