Ошибка типа II

Что такое ошибка второго рода?

Ошибка типа II, обычно называемая ошибкой «β», представляет собой вероятность сохранения неверного фактического утверждения. Это ошибка ложного срабатывания, т. е. утверждение фактически ложно, и мы уверены в этом.

Оглавление

• Что такое ошибка второго рода?
  • Объяснение
  • Пример ошибки типа II
  • Как возникает ошибка типа II?
  • Можно ли избежать ошибок типа II?
  • Важность
  • Ошибка типа I против ошибки типа II
  • Заключение
  • Рекомендуемые статьи

Объяснение

Ошибки типа обычно используются для создания гипотезы, определения решения на основе вероятности их появления и определения фактической корректировки данных, которые структурировали гипотезу.

На диаграмме показано создание нулевой гипотезыНулевая гипотезаНулевая гипотеза предполагает, что данные выборки и данные населения не имеют различий, или, говоря простыми словами, она предполагает, что утверждение, сделанное человеком в отношении данных или населения, является абсолютной истиной и всегда верно . Таким образом, даже если выборка берется из населения, результат, полученный в результате изучения выборки, будет таким же, как и предположение. Читать далее, альтернативная гипотеза, среднее значение выборки и вероятность ошибки.

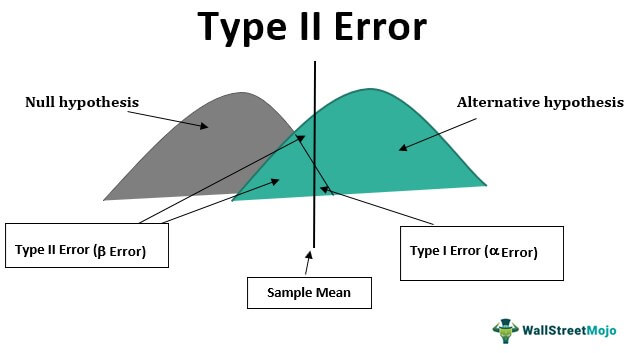
Каждый тест, который мы проводим, всегда имеет вероятность ошибки при принятии решения, и такое решение может быть ошибкой типа I или типа II. Проще говоря, принимая решения, мы можем отвергать правильные факты или принимать неправильные. Отвержение правильных фактов — это ошибка первого рода, а принятие неверных фактов — ошибка второго рода. Эта ошибка может быть очень опасной в корпоративном мире, поскольку полный анализ и эксперимент могут быть ошибочными, если сама база неверна.

Ниже приведена матрица того, какой тип ошибки можно совершить, если факты будут приняты неправильно:

Было принято решение сохранитьПринято решение об отказе (Положительный) (Отрицательный) Нулевая гипотеза верна Истинно положительная Истинно отрицательная (1-a) = ошибка типа I Нулевая гипотеза ложная Ложноположительная ложноотрицательная (β) = ошибка типа II (1 – β) популяция сравнительно очень мала, чтобы обнаружить

Если тенденция к изменению не видна в самой популяции, то любая проверка гипотез Проверка гипотез Проверка гипотез является статистическим инструментом, который помогает измерить вероятность правильности результата гипотезы, полученного после выполнения гипотезы на выборочных данных. Это подтверждает правильность полученных результатов первичной гипотезы. Такой сценарий приведет к принятию неверных фактов, что приведет к ошибкам второго рода.

№ 2. Размер выборки охватывает очень небольшую часть населения.

Выборка должна представлять всю совокупность. Таким образом, если выборка не является идеальным представлением генеральной совокупности, маловероятно, что она даст правильный анализ. Аналитик не сможет определить правильные факты. В результате они будут полагаться на неправильные факты, что приведет к ошибке типа II.

#3 – Неправильный выбор образца

Как правило, во всем мире используется случайная выборка, поскольку она считается одним из самых объективных методов отбора выборки. Однако во многих случаях это приводит к неправильному выбору образцов. В результате это приводит к неправильному охвату населения и приводит к ошибке второго рода.

Можно ли избежать ошибок типа II?

# 1 – Повторяйте анализ, пока не достигнете требуемой значимости

Значимость указывает, является ли нулевая гипотеза фактически верной или нет. В конце всех анализов принимается нулевая гипотеза и проверяется правильность фактов. Однако часто только один анализ не может достичь такой значимости. Такой односторонний анализ может привести к ошибкам типа I или типа II. С другой стороны, если при повторном анализе будут получены одни и те же выходные данные, можно гарантировать отсутствие ошибок.

#2 – При каждом повторении анализа меняйте размер критерия значимости

Как обсуждалось в пункте 1, значимость показывает правильность нулевой гипотезы. Если обнаруживается, что выборка недостаточно охвачена, можно повторить, что размер значимости увеличивается. Это поможет понять поведение и избежать ошибки типа II.

№ 3. Уровень альфа около 0,1 является идеальным.

Как правило, альфа около 0,1 приводит к отклонению гипотезы. Любой отказ позволит несколько проверок. В результате вероятность возникновения ошибок снижается. Ошибка типа II возникает, когда что-то принимается неправильно. Если возможности для принятия нет, такой ошибки не произойдет.

Важность

• Это более опасно по сравнению с ошибками первого рода.
• Любой анализ может быть разработан на основе нескольких необходимых деталей и основных предположений. В конце гипотезы можно определить, соответствует ли тестовая статистика данному факту или нет. Такие особенности теста будут отображать, эквивалентны ли выборочные средние среднему значению генеральной совокупности.
• Если кажется, что нулевая гипотеза достигает значимости из-за какой-то ошибки в анализе, можно принять этот факт в нулевой гипотезе.
• Однако в действительности такая нулевая гипотеза должна быть неприемлемой. В результате нужно быть очень уверенным, принимая утверждение нулевой гипотезы. Повторно проверяя его, можно получить большее значение, чтобы повысить правильность факта.

Ошибка типа I против ошибки типа II

Ниже приведены основные различия между двумя типами ошибок:

старший нетОшибка I типаОшибка второго рода1 Это происходит, когда правильная нулевая гипотеза не принимается. Это происходит, когда принимается неверная нулевая гипотеза.2 Такие ошибки действительно отрицательные. Такие ошибки являются ложноположительными.3Обозначается альфа. Обозначается бета4Нулевая гипотеза и ошибка 1-го рода Альтернативная гипотеза и ошибка 2-го рода5Если результирующий эффект этой ошибки хуже, чем ошибка типа I, следует рассматривать альфа со значением выше 0,10. Если результирующий эффект ошибки типа I хуже, следует установить альфа со значением ниже 0,01.

Заключение

Ошибка II рода — это ложноотрицательный результат, возникающий в результате принятия неверной нулевой гипотезы. В практическом мире такие ошибки приводят к провалу всего проекта, поскольку база неточна. Более того, такой базой могут быть как детали, факты или предположения, ставящие под угрозу полноту анализа.

Рекомендуемые статьи

Эта статья представляет собой руководство по ошибке типа II и ее определению. Здесь мы обсуждаем примеры, объяснения, как это происходит и как этого избежать. Вы можете узнать больше о финансировании из следующих статей: –

• P-значение
• Дисперсионный анализ в Excel
• Т-тест
• Статистика