Мера М2

Что такое показатель М2?

Показатель M2 — это расширенная и более полезная версия коэффициента Шарпа, которая дает нам доходность портфеля с поправкой на риск путем умножения коэффициента Шарпа на стандартное отклонение любого эталонного рыночного индекса и последующего добавления к нему безрисковой доходности.

Оглавление

• Что такое показатель М2?
  • Формула и шаги для расчета меры M2
  • Пример расчета меры M в квадрате
  • Преимущества
  • Недостатки
  • Важные моменты измерения M2
  • Заключение
  • Рекомендуемые статьи

Формула и шаги для расчета меры M2

Для расчета M2, во-первых, будет рассчитан коэффициент Шарпа (годовой). Затем рассчитанный коэффициент Шарпа будет использоваться для получения квадрата М путем умножения коэффициента Шарпа на стандартное отклонение эталона. Здесь эталон будет выбран лицом, вычисляющим показатель M2.

Примерами стандартных ориентиров могут быть индекс MSCI World, индекс S&P 500 или любой другой широкий индекс. После умножения коэффициента Шарпа на стандартное отклонение эталона безрисковая ставкаБезрисковая ставкаБезрисковая ставка представляет собой минимальную норму прибыли, ожидаемую инвестором от инвестиций с нулевым риском. Это государственные облигации развитых стран, либо казначейские облигации США, либо государственные облигации Германии. Хотя его не существует, потому что каждая инвестиция имеет определенную долю риска. Подробнее о доходе будет добавлено.

Ниже приведены шаги или формулы для расчета показателя M2.

Шаг 1: Расчет коэффициента Шарпа (в годовом исчислении)

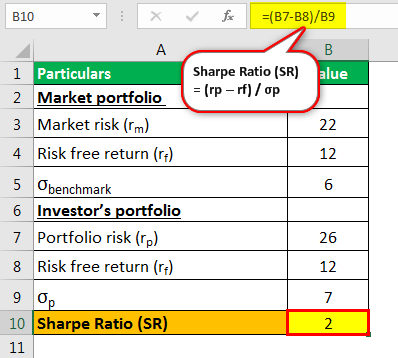
Формула коэффициента Шарпа Формула коэффициента Шарпа Формула коэффициента Шарпа рассчитывает превышение доходности над безрисковой доходностью на единицу волатильности портфеля. Безрисковая норма доходности вычитается из ожидаемой доходности портфеля и делится на стандартное отклонение портфеля. Коэффициент Шарпа = (Rp – Rf)/ σp (SR) = (rp – rf) / σp

Где,

• rp = доходность портфеля
• rf = безрисковая норма доходности
• σp = стандартное отклонение избыточной доходности портфеля.

Шаг 2: Умножение коэффициента Шарпа, рассчитанного на шаге 1, на стандартное отклонение эталона

= SR * контрольный показатель

Где,

• σbenchmark = стандартное отклонение эталона

Шаг 3: Добавление безрисковой нормы доходности к результату, полученному на шаге 2.

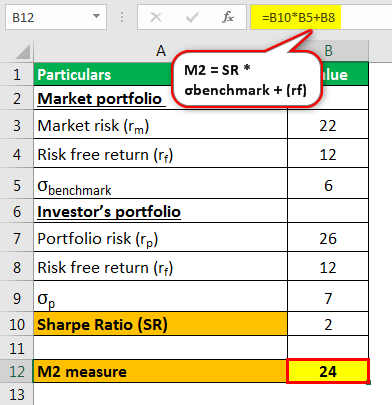
M квадрат меры = SR * σbenchmark + (rf)

С помощью уравнения, полученного выше для расчета показателя Модильяни-Модильяни, можно увидеть, что показатель M2 представляет собой избыточную доходность, взвешенную по стандартному отклонению эталона и портфеля, увеличивающемуся с безрисковой нормой доходности.

Пример расчета меры M в квадрате

Используйте рыночный портфель с портфелем инвесторов, чтобы вычислить меру Модильяни-Модильяни.

Данный:

Рыночный портфель:

• Рыночный риск (rm): 22
• Безрисковая доходность (rf): 12
• σбенч: 6

Портфель инвестора:

• Риск портфеля (RP): 26%
• Рис бесплатный возврат (рф): 12%
• сп: 7

Расчет производительности Модильяни с поправкой на риск (RAP)

1. Расчет коэффициента Шарпа

   

   Коэффициент Шарпа (SR) = (26 – 12) / 7
   Коэффициент Шарпа (SR) = 14/7
   Коэффициент Шарпа (SR) = 2

2. Расчет меры М2

   

   M2 = SR * σbenchmark + (rf)
   М2 = 12 + (12)
   М2 = 24 %

Преимущества

1. Это показатель производительности с поправкой на риск, который легко интерпретировать.
2. Показатель M2 более полезен по сравнению с коэффициентом Шарпа, из которого он получен, потому что неудобно интерпретировать коэффициент Шарпа, когда он отрицательный.
3. Кроме того, может оказаться затруднительным сравнивать коэффициенты Шарпа непосредственно для различных инвестиций. Например, если кто-то хочет сравнить два разных портфеля, один из которых имеет коэффициент Шарпа 0,60, а другой -0,60, то будет трудно сделать вывод, насколько хуже второй портфель.
4. То же самое и в случае другого показателя, такого как коэффициент ТрейнораКоэффициент ТрейнораКоэффициент Трейнора похож на коэффициент Шарпа и рассчитывает избыточную доходность по сравнению с безрисковой доходностью на единицу волатильности портфеля, используя бета, а не стандартное отклонение в качестве меры риска. В результате он дает избыточную доходность по сравнению с безрисковой нормой доходности на единицу коэффициента бета всего портфеля инвестора.Подробнее, коэффициент СортиноКоэффициент СортиноКоэффициент Сортино — это статистический инструмент, используемый для оценки рентабельности инвестиций для данного уровень плохого риска. Он рассчитывается путем вычитания безрисковой ставки доходности из ожидаемой доходности и деления результата на отрицательное стандартное отклонение портфеля (отклонение в сторону понижения) и другие коэффициенты, которые рассчитываются в терминах коэффициентов. Эта проблема решена в доходности Модильяни с поправкой на риск, поскольку она выражается в единице процентной доходности, которая может быть мгновенно и легко интерпретирована всеми инвесторами.
5. Таким образом, легко понять разницу между двумя или более инвестиционными портфелями. которые пропорциональны профилю риска инвестора.Подробнее. Так как значения M2 для портфеля 1 составляют 5,4%, а для второго портфеля — 5,9%, то это показывает, что существует разница в 0,5% доходности с поправкой на риск и скорректированной на риск относительно эталонного портфеля.
6. Таким образом, это помогает в сравнении двух разных портфелей.

Недостатки

1. Данные, используемые для расчета показателей M2, включают только исторический риск.
2. Управляющий портфелем Управляющий портфелем Управляющий портфелем — это эксперт по финансовому рынку, который занимается стратегическим проектированием инвестиционных портфелей. Читать далее может манипулировать показателями, направленными на повышение их истории доходности с поправкой на риск.

Важные моменты измерения M2

1. Расчетная доходность портфеля Расчетная доходность портфеля Формула доходности портфеля рассчитывает доходность всего портфеля, состоящего из различных отдельных активов. Формула рассчитывается путем вычисления рентабельности инвестиций в отдельный актив, умноженной на соответствующую весовую категорию в общем портфеле, и сложения всех результатов вместе. Rp = ∑ni=1 и далее будет равно показателю M2, когда стандартное отклонение портфеля равно стандартному отклонению эталона. Обычно это происходит, когда портфель отслеживает индекс.
2. Мера М-квадрат также имеет альтернативу, где систематический рискСистематический рискСистематический риск определяется как риск, присущий всему рынку или всему рыночному сегменту, поскольку он влияет на экономику в целом и не может быть диверсифицирован, поэтому он также известен как вместо полного компонента волатильности будет использоваться «недиверсифицируемый риск», «рыночный риск» или даже «риск волатильности». Однако то же самое будет хорошим индикатором только в том случае, если рассматриваемый портфель является хорошо диверсифицированным портфелем, потому что недостаточная диверсификация может привести к недооценке рискованности портфеля, поскольку некоторый идиосинкразический рискИдиосинкразический рискИдиосинкразический риск возникает из-за переменных или условий, влияющих на стоимость портфеля. единичный, множественный или редкий актив конкретной компании или сектора с течением времени, а не рыночный риск. В этом случае будет оставлено больше информации.
3. Показатель M2 выводится непосредственно из коэффициента Шарпа, поэтому любое упорядочение портфеля с использованием показателя M2 будет точно таким же, как упорядочение портфеля с использованием коэффициента Шарпа.
4. Показатель M2 помогает в измерении доходности портфелей после корректировки связанного с ним риска, т. е. он измеряет доходность с поправкой на риск оцениваются и корректируются таким образом, чтобы человек мог решить, стоит ли инвестировать, учитывая все риски для вложенного капитала. Узнайте больше о различных инвестиционных портфелях по сравнению с эталоном.
5. Мера M2 также иногда известна как M-квадрат, мера Модильяни-Модильяни, RAP или производительность с поправкой на риск Модильяни.
6. Показатель M2 можно интерпретировать как разницу между масштабированной избыточной доходностью портфеля и рынком, где масштабированный портфель имеет такую ​​же волатильность, как и рыночная.
7. Показатель M в квадрате рассчитывается на основе известного и широко используемого коэффициента Шарпа Коэффициент Шарпа Коэффициент Шарпа, также известный как показатель Шарпа, представляет собой финансовый показатель, используемый для описания избыточного дохода инвесторов для дополнительной волатильности, возникающей при удерживании рискованного актива. Вы можете рассчитать его по формуле: Коэффициент Шарпа = {(Средняя норма доходности инвестиций – Безрисковая ставка)/Стандартное отклонение доходности инвестиций} читать далее» с дополнительным преимуществом, заключающимся в том, что он выражен в единицах процентного дохода, что делает его интуитивно понятный для интерпретации пользователем.

Заключение

Измерение M2 полезно для понимания того, насколько хорошо портфель вознаграждает инвестора при заданном размере принятого риска по отношению к эталонному портфелю и безрисковой норме доходности. Таким образом, если рассматривается инвестиция, имеющая больший риск, чем эталонный портфель, с небольшим преимуществом в производительности, то она может иметь меньшую доходность с поправкой на риск по сравнению с другим портфелем, в котором риск меньше по сравнению с некоторым эталонным портфелем, но имеющий аналогичная сумма возврата. Это легко интерпретировать и полезно по сравнению с двумя или более портфелями пользователя.

Рекомендуемые статьи

Это было руководство к тому, что такое M2 Measure. Здесь мы обсудим формулу для расчета M в квадрате вместе с примерами, преимуществами и недостатками. Вы можете узнать больше об инвестиционном банкинге из следующих статей –

• Объединенные фонды
• Примеры стандартного отклонения
• Индекс Паше
• Квантовое инвестирование
• Модифицированный Дитц