Формула экспоненциального роста

Формула для расчета экспоненциального роста

Экспоненциальный рост относится к увеличению из-за объединения данных с течением времени. Следовательно, он следует кривой, представляющей показательную функцию.

Окончательное значение = Начальное значение * (1 + Годовой темп роста/Количество сложных процентов )Нет. лет * № рецептуры

Однако в случае непрерывного начисления Непрерывное начисление Формула непрерывного начисления отражает проценты, получаемые при постоянном начислении процентов в течение бесконечного числа периодов. Четыре переменные, используемые для его расчета, — это основная сумма, время, процентная ставка и номер периода начисления сложных процентов. Более того, уравнение вычисляет окончательное значение путем умножения начального значения и экспоненциальной функции, возведенной в степень годового скорость роста в количестве лет.

Математически это представляет, как показано ниже,

Окончательное значение = Начальное значение * e Годовой темп роста * №. лет.

Оглавление

• Формула для расчета экспоненциального роста
  • Расчет экспоненциального роста (шаг за шагом)
  • Пример
    • Ежемесячное начисление процентов
    • Ежеквартальное начисление процентов
    • Полугодовое начисление процентов
    • Ежегодное начисление сложных процентов
    • Непрерывное компаундирование
  • Калькулятор
  • Актуальность и использование
  • Рекомендуемые статьи

Расчет экспоненциального роста (шаг за шагом)

Можно рассчитать экспоненциальный рост, используя следующие шаги:

1. Во-первых, определите начальное значение, для которого необходимо рассчитать конечное значение. Например, это может быть текущая стоимость денег при расчете временной стоимости денег.

2. Затем определите годовой темп роста, который можно решить в зависимости от типа приложения. Например, если формула предназначена для расчета формулы будущей стоимости депозита, то темп роста будет равен норме доходности, ожидаемой от рыночной ситуации.
   

3. Выяснена продолжительность роста с точки зрения количества лет, т. е. как долго стоимость будет сохраняться при такой крутой траектории роста.

4. Теперь определите количество периодов начисления процентов в год. Начисление может быть ежеквартальным, полугодовым, годовым, непрерывным и т.д.

5. Наконец, экспоненциальный рост заключается в вычислении конечного значения путем начисления начального значения (шаг 1) с использованием годового темпа роста (шаг 2), количества лет (шаг 3) и числа, начисленного в год (шаг 4). , как показано выше.
   

С другой стороны, формула для непрерывного начисления процентов состоит в том, чтобы вычислить конечное значение путем умножения начального значения (Шаг 1) и экспоненциальной функции, возведенной в степень годового темпа роста (Шаг 2) за несколько лет (Шаг 3), как показано выше.

Пример

.free_excel_div{фон:#d9d9d9;размер шрифта:16px;радиус границы:7px;позиция:относительная;margin:30px;padding:25px 25px 25px 45px}.free_excel_div:before{content:””;фон:url(центр центр без повтора #207245;ширина:70px;высота:70px;позиция:абсолютная;верх:50%;margin-top:-35px;слева:-35px;граница:5px сплошная #fff;граница-радиус:50%}

Вы можете скачать этот шаблон Excel формулы экспоненциального роста здесь – Формула экспоненциального роста Шаблон Excel
Возьмем пример Давида. Он положил 50 000 долларов на свой банковский счет на три года под 10% годовых. Определите стоимость депонированных денег через три года, если начисление процентов:

1. Ежемесячно
2. Ежеквартальный
3. Полугодовой
4. Ежегодно
5. Постоянно

Ежемесячное начисление процентов

Количество начислений в год = 12 (начиная с месяца)

Расчет экспоненциального роста, т. е. стоимости депонированных денег через три года, выполняется по приведенной выше формуле:

• Окончательная стоимость = 50 000 долларов США * (1 + 10%/12)3 * 12

Расчет будет-

• Окончательная стоимость = 67 409,09 долларов США.

Ежеквартальное начисление процентов

Количество начислений в год = 4 (начиная с квартала)

Расчет экспоненциального роста, т. е. стоимости депонированных денег через три года, выполняется с использованием приведенной выше формулы:

Окончательная стоимость = 50 000 долларов США * (1 + 10%/4)3 * 4

Расчет будет-

• Окончательная стоимость = 67 244,44 доллара США.

Полугодовое начисление процентов

Количество рецептур в год = 2 (начиная с полугодия)

Стоимость депонированных денег через три года рассчитывается по приведенной выше формуле:

Окончательная стоимость = 50 000 долларов США * (1 + 10%/2)3 * 2

Расчет экспоненциального роста будет-

• Окончательная стоимость = 67 004,78 долларов США.

Ежегодное начисление сложных процентов

Количество начислений в год = 1 (начиная с годового)

Расчет экспоненциального роста, т. е. стоимости депонированных денег через три года, выполняется с использованием приведенной выше формулы:

Окончательная стоимость = 50 000 долларов США * (1 + 10%/1)3 * 1

Расчет экспоненциального роста будет-

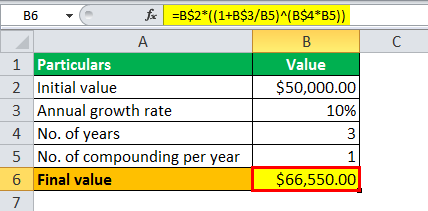
• Окончательная стоимость = 66 550,00 долларов США.

Непрерывное компаундирование

Поскольку непрерывное начисление процентов, стоимость депонированных денег через три года рассчитывается по приведенной выше формуле:

Окончательное значение = Начальное значение * e Годовой темп роста * №. лет

Окончательная стоимость = 50 000 долларов США * e 10% * 3

Расчет экспоненциального роста будет-

• Окончательная стоимость = 67 492,94 доллара США.

Калькулятор

Вы можете использовать следующий калькулятор экспоненциального роста.

.cal-tbl td{ верхняя граница: 0 !важно; }.cal-tbl tr{ высота строки: 0.5em; } Только экран @media и (минимальная ширина устройства: 320 пикселей) и (максимальная ширина устройства: 480 пикселей) { .cal-tbl tr{ line-height: 1em !important; } } Начальное значение Годовой темп роста №. № рецептуры лет Формула экспоненциального роста =

Формула экспоненциального роста = начальное значение * (1 + годовой темп роста/количество начислений) лет*№ начисления 0 * (1 +0/0)0*0 = 0

Актуальность и использование

Финансовый аналитик должен понимать уравнение экспоненциального роста, поскольку оно в первую очередь рассчитывает сложную доходность. Грандиозность этой концепции в финансах демонстрирует способность сложных процентов создавать большие суммы при значительно меньшем начальном капитале. По той же причине он имеет большое значение для инвесторов, которые верят в длительные периоды владения.

Рекомендуемые статьи

Эта статья представляет собой руководство по формуле экспоненциального роста. Здесь мы обсуждаем вычисление экспоненциального роста с примерами и загружаемыми листами Excel. Вы можете узнать больше о финансировании из следующих статей: –

• Экспоненциальное распределениеЭкспоненциальное распределениеЭкспоненциальное распределение относится к непрерывному и постоянному распределению вероятностей, которое фактически используется для моделирования периода времени, в течение которого человек должен ждать, прежде чем произойдет данное событие. Это распределение является непрерывным аналогом геометрического распределения, которое отличается от других.Подробнее
• Формула роста в Excel
• Рассчитать устойчивый темп роста
• Формула темпа роста дивидендов